728x90
베이지안 확률(Bayesian Probability)
- 세상에 반복할 수 없는 혹은 알 수 없는 확률
- 새로운 정보를 토대로 어떤 사건이 발생했다는 주장에 신뢰도를 갱신하는 방법 -> 일어나지 않은 일에 대한 확률을 사건과 관련이 있는 여러 확률을 통해 추정하는 것
빈도 확률(Frequentist probability), 베이지안 확률(Bayesian probability)
"동전을 던졌을 때 앞면이 나올 확률은 50%이다 "에 대한 각각의 확률 관점
- 베이지안 주의
- 동전이 앞면이 나왔다는 주장에 대한 신뢰도는 50%
- 동전 던지기가 아닌 확률을 알기 어려운 사건에 대해서 베이지안을 사용함
- 화산이 폭발할 확률과 같이 빈도 확률의 개념을 적용할 수 없는 경우 사건과 관련이 있는 여러 확률을 이용하여 새롭게 일어날 사건을 추정하는 것
- 빈도주의
- 동전을 100번 던졌을 때 45번이 나왔으면 확률은 \( \frac{45}{100} \)
- 동전을 100번 던졌을 때 55번이 나왔으면 확률은 \( \frac{55}{100} \)
- 위와 같이 시행횟수를 반복하여 빈도수를 측정하는 것
정의
베이즈 정리라고 불리며 종속적 관계에 놓인 사건들을 기반으로 확률을 구한다.
- 두 확률 변수의 사전 확률과 사후 확률 사이의 관계를 나타내는 정리
- 사전확률 \( P(A) \)와 우도확률 \( P(B \mid A) \)를 안다면 사후확률 \( P(A \mid B) \)를 알 수 있음
$$ P(A \mid B)= \frac{P(B \mid A)P(A)}{P(B)} $$
- A: 원인
- B: 결과
- \( P(A) \) 사전 확률(Prior probability): 결과가 나타나기 전에 결정되어 있는 A의 확률
- \( P(B \mid A) \) 우도 확률(likelihood probability): A가 발생하였다는 조건하에 B가 발생할 확률
- \( P(A \mid B) \) 사후 확률(posterior probability): B가 발생하였다는 조건하에 A가 발생하였을 확률
예제
problem
- Premise
- 질병 A 에 대한 발병률은 0.1%
- 질병 A에 걸렸을 때 질병이 있다고 검진할 확률 99.9%
- 질병 A에 걸리지 않았을 때 질병이 없다고 검진할 확률 98%
- Question
- 질병 A에 걸렸다고 검진받았을 때, 정말 질병 A에 걸렸을 확률을 구하시오. P(H|E)
Solution
- Hypothesis : True -> 병에 걸렸다.
- Evidence : Positive -> 병에 걸리고 양성이 나왔다.
P(H) = 0.001
P(E|H) = 0.98
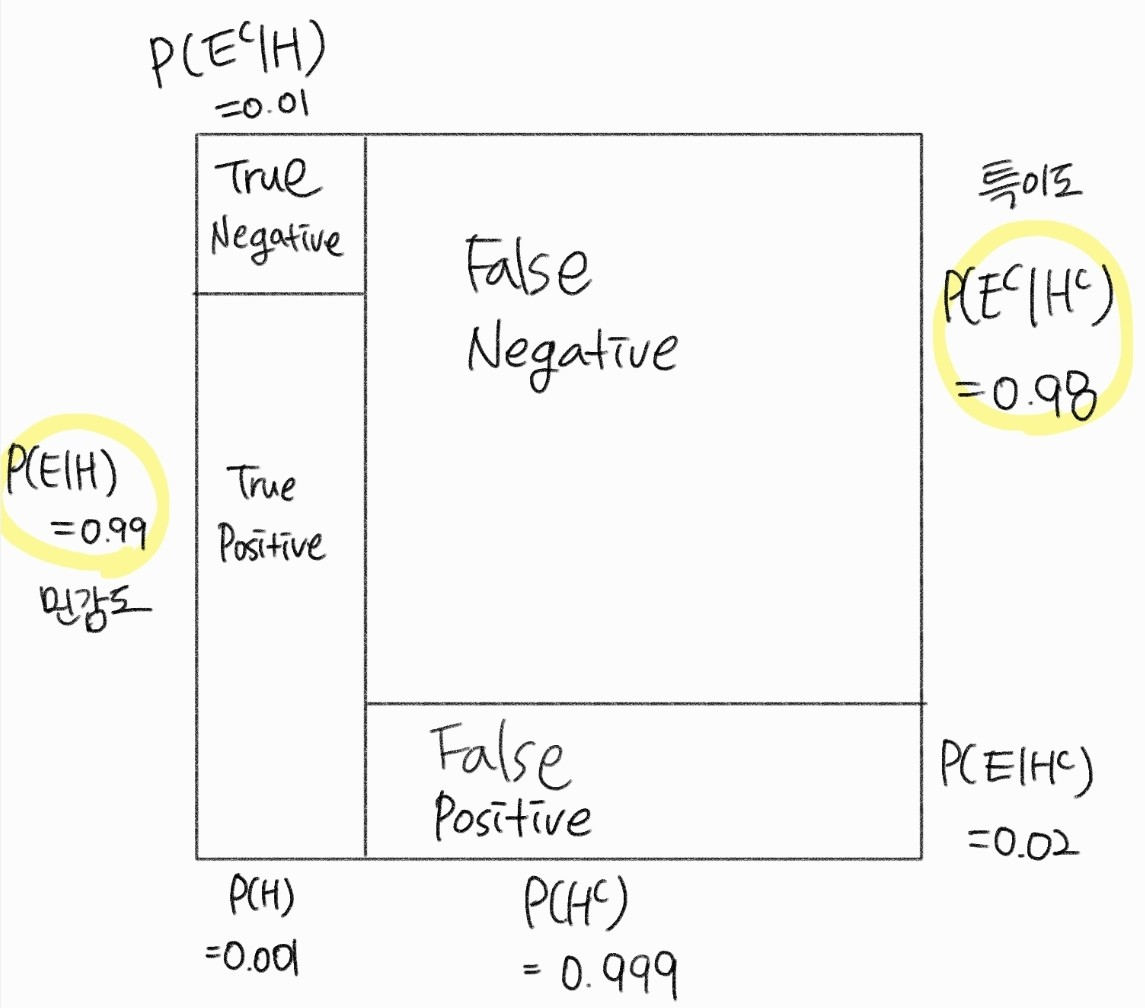
민감도 : 진짜 감염자들을 대상으로 검사했을 때 자가검사키트로 양성이 진단되는 비율
특이도 : 진짜 비감염자들을 대상으로 검사했을 때 자가검사키트로 음성이 진단되는 비율

약 4%의 확률로 병에 걸렸을 것이다.
Hypothesis 다시 생각하기
- 앞에서의 P(H) = 0.001
- 위의 Problem의 사후 확률인 P(H|E)를 사전 확률로 이용하여 다시 한번 더 계산한다.
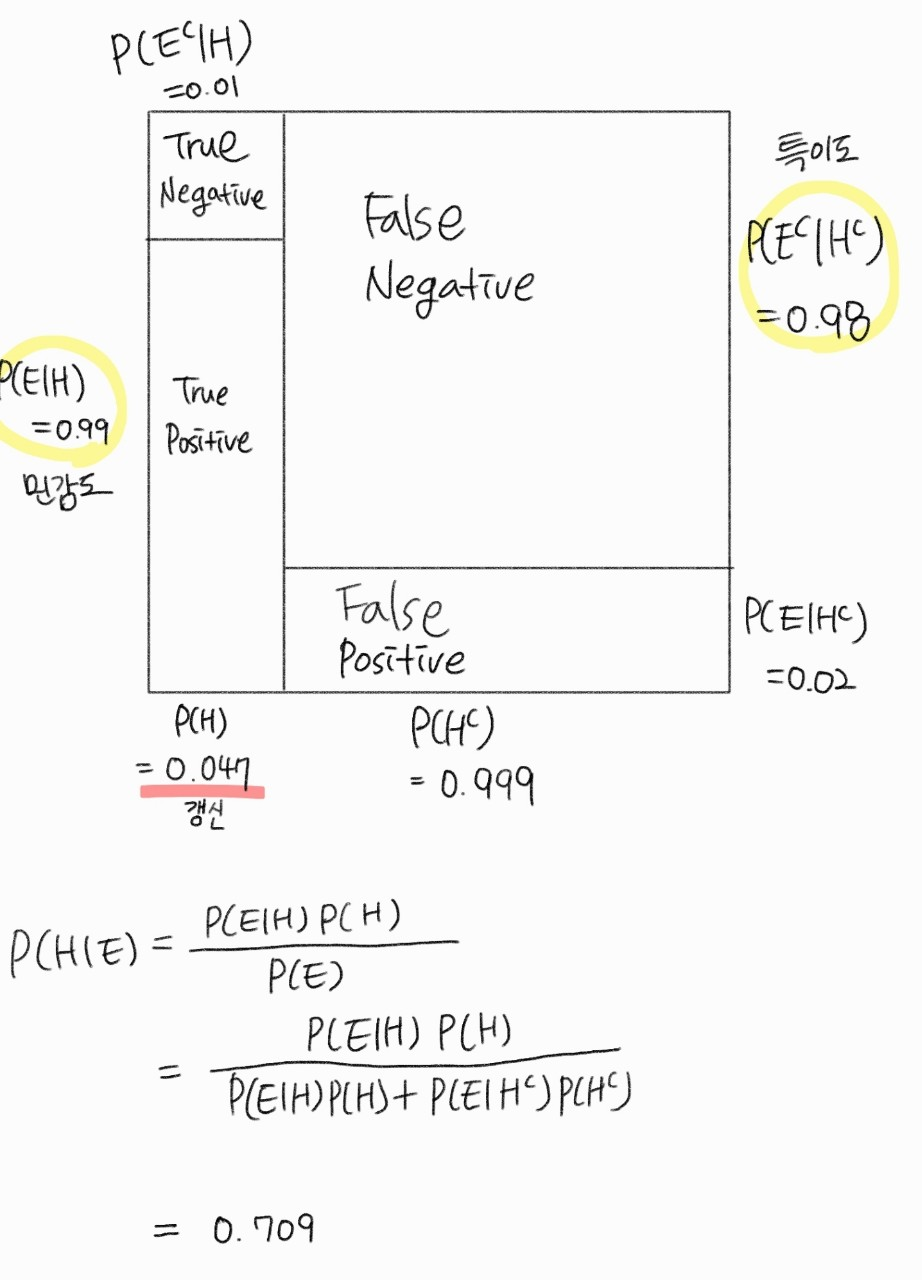
약 70%의 확률로 병에 걸렸을 것이다.
728x90
'Machine Learning > 이론' 카테고리의 다른 글
| [ML] Overfitting, Underfitting (0) | 2022.08.17 |
|---|---|
| Hypothesis and Inference, p-value (0) | 2022.08.11 |
| [Statistics] 중심 경향성 (0) | 2022.08.09 |
| [ML] 경사 하강법 (0) | 2021.04.01 |
| [ML] 선형 회귀 (0) | 2021.03.30 |
