728x90
선형 회귀란 독립 변수 x 를 사용해 종속 변수 y 값을 예측하는 작업을 뜻한다.
선형 회귀의 예측선은 일직선을 그리기 때문에 y = ax + b 으로 가설을 세우는 게 가능하다.
예측선을 정확하게 그으려면 상수 a와 b를 추정해야한다.
최소제곱법을 적용하여 기울기 a 와 b를 바로 구할 수 있다.
a = (x - x평균)(y - y평균)의 합 / (x - x평균)^2 의 합
b = y의 평균 - (x의 평균 * a)
예시를 들어 x를 공부한 시간 y를 성적이라고 하였을 때
| 공부한 시간 | 2 | 4 | 6 | 8 |
| 성적 | 81 | 93 | 91 | 97 |
| 예측 값 | 83.6 | 88.2 | 92.8 | 97.4 |
이러한 표가 있다고 가정하자.
a = ( 2 - 5 )*( 81 - 90.5 )+( 4 - 5 )*( 93 - 90.5 )+( 6 - 5 )*( 91 - 90.5 )+( 8 - 5 )*( 97 - 90.5 ) /
( 2 - 5 )^2+( 4 - 5 )^2+( 6 - 5 )^2+( 8 - 5 )^2 = 46/20 = 2.3
b = 90.5 - (2.3*5) = 79
a = 2.3, b = 79의 값을 구했고 y = 2.3x + 79 로 예측이 가능하다 이제 이걸 코드로 나타내 볼 것이다.
import numpy as np
import math
import matplotlib.pyplot as plt
X =[2,4,6,8]
Y = [81,93,91,97]
X_mean = np.mean(X)
Y_mean = np.mean(Y)
a = sum([(X[i]-X_mean)*(Y[i]-Y_mean)for i in range(len(X))])/sum([math.pow(i - X_mean,2) for i in X])
b = Y_mean - (X_mean*a)
y_e = [(a*i+b) for i in X]
#그래프 그리기
plt.plot(X,Y,'ro')
plt.plot(X,y_e,'bo')
plt.plot(X,y_e)
plt.show()
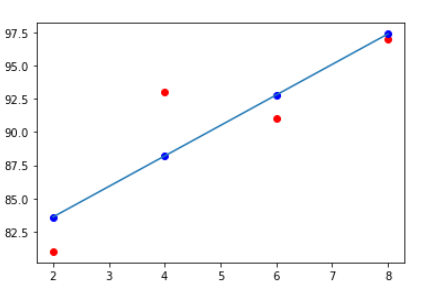
빨간 점은 점수이고 파란 점은 예측 값이다.
나중에 경사 하강법을 통해 오차를 줄이는 방향으로 수정할 것이다.
오차 = 실제 값 - 예측 값

제곱을 해주어 음수를 없애준다.

728x90
'Machine Learning > 이론' 카테고리의 다른 글
| [ML] Overfitting, Underfitting (0) | 2022.08.17 |
|---|---|
| Hypothesis and Inference, p-value (0) | 2022.08.11 |
| [통계] 베이지안 이론 Bayesian theory (0) | 2022.08.10 |
| [Statistics] 중심 경향성 (0) | 2022.08.09 |
| [ML] 경사 하강법 (0) | 2021.04.01 |
