728x90
Hypothesis
- 귀무 가설 (Null Hypothesis) : 가설 검정에서 기본 입장
- 대립 가설 (Alternative alt Hypothesis) : 귀무 가설과 대비되는 입장
가설을 세우고 추론해보자!
귀무 가설 : 1 ~ 10 숫자 카드를 랜덤하게 뽑았을 때 5가 나올 확률은 \( \frac{1}{10} \)이다.
대립 가설 : 1 ~ 10 숫자 카드를 랜덤하게 뽑았을 때 5가 나올 확률은 \( \frac{1}{10} \)가 아니다.
베르누이 : 2가지의 결과값만 갖는 것
1 ~ 10 숫자 카드 중에서 5를 뽑을 때 1이라고 한다면 1000번 실행하였을 때 5가 나올 확률
import random
def bernoulli_trial(p) :
return 1 if random.randint(1,10) == p else 0
def binomial(n, p) -> int:
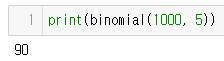
return sum(bernoulli_trial(p) for _ in range(n))print(binomial(1000, 5))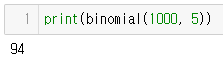
from collections import Counter
import matplotlib.pyplot as plt
import math
# cdf
def normal_cdf(x, mu, sigma):
return (1 + math.erf((x - mu) / math.sqrt(2) / sigma)) / 2
def binomial_histogram(p, n, num_points):
data = [binomial(n, p) for _ in range(num_points)]
histogram = Counter(data)
plt.bar([x - 0.4 for x in histogram.keys()],
[v / num_points for v in histogram.values()],
0.8,
color='0.75')
mu = sum(data)/len(data)
sigma_sum = 0
for da in data:
sigma_sum += (da-mu)**2
sigma = sigma_sum / len(data)
sigma = math.sqrt(sigma)
xs = range(min(data), max(data) + 1)
ys = [normal_cdf(i + 0.5, mu, sigma) -
normal_cdf(i - 0.5, mu, sigma) for i in xs]
plt.plot(xs, ys)
plt.title("Binomial Distribution vs. Normal Approximation")
plt.show()
binomial_histogram(5, 1000, 1000)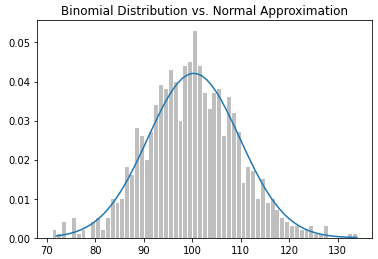
(1 ~ 10 숫자 카드에서 5뽑기를 1000번 진행하였을 때 5는 100번 정도 나왔다)
위의 행위를 1000번 반복한다면
평균은 100이고 분산은 9.486이 나온다
import random
import numpy as np
def normal_approximation_to_binomial(n, p):
mu = p * n
sigma = math.sqrt(p * (1 - p) * n)
return mu, sigma
# call function
# (500.0, 15.811388300841896)
normal_approximation_to_binomial(1000, 0.1)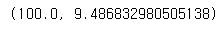
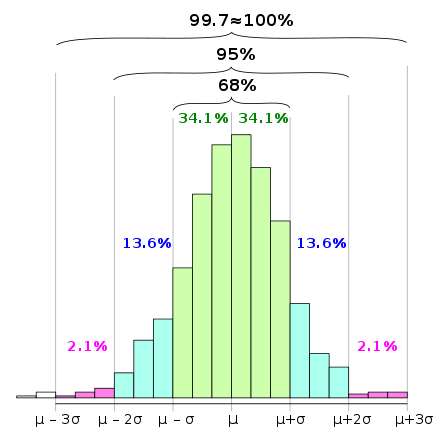
68%의 이항 확률 변수는 100 \( \pm \) 9.486
95%의 이항 확률 변수는 100 \( \pm \) 18.912
가설 검증
제 1종 오류
- 귀무 가설이 참인데 기각할 경우
제 2종 오류
- 귀무 가설이 거짓인데 기각하지 않은 경우
P-value
- 귀무 가설이 옳다고 가정하고 실제 관측된 값보다 극단적인 값이 나올 확률이다. 우연을 평가함.
- 실험에서 평균 98에 표준편차 9가 나왔다. 여기서 나온 평균 98이 모평균이 될 수 있을까?
- 가설 검증은 전체 데이터에서 일부만을 추출하여 평균을 내는 것이기 때문에 추출 데이터의 평균이 전체 데이터의 평균에서 멀어질 수 있다.
- 모평균이 100이라는 가정하에 추출 데이터의 평균이 100에서 멀어지면 모평균이 100이 아닐지도 모른다고 생각하게 됨

p-value 핑크색 부분
모집단 분포에서 임의로 값을 선택할 때, 핑크색 부분을 가져올 확률
유의 수준(alpha) = 0.05, 5%
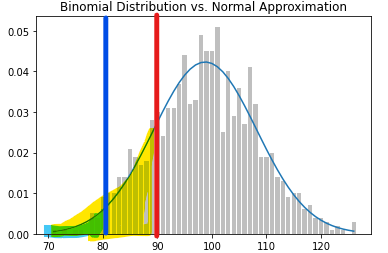
노란 부분 - p-value
파란 부분 - alpha
p-value > alpha
90은 모집단 분포의 일부이다.
728x90
'Machine Learning > 이론' 카테고리의 다른 글
| 머신러닝 Machine Learning Bias, Variance (0) | 2022.08.17 |
|---|---|
| [ML] Overfitting, Underfitting (0) | 2022.08.17 |
| [통계] 베이지안 이론 Bayesian theory (0) | 2022.08.10 |
| [Statistics] 중심 경향성 (0) | 2022.08.09 |
| [ML] 경사 하강법 (0) | 2021.04.01 |
