통계학
산술적 방법을 기초로 하여, 주로 다량의 데이터를 관찰하고 정리 및 분석하는 방법을 연구하는 수학의 한 분야
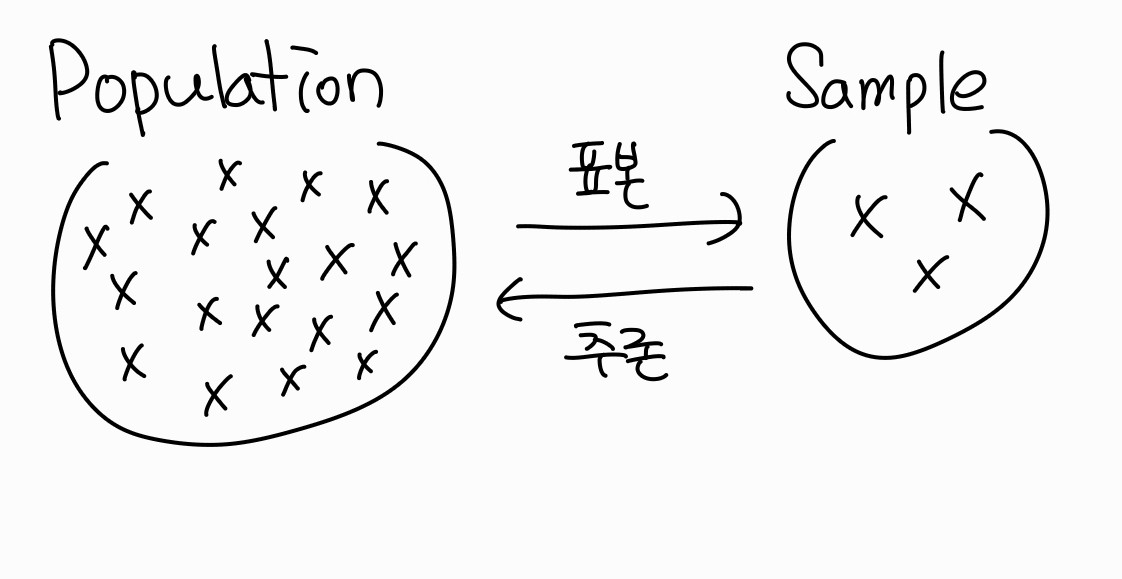
모집단 (Population)
연구자가 알고 싶어 하는 대상이 되는 모든 개체들을 모은 집합 (집단 전체)
표본 (Sample)
모집단에서 측정한 일부분의 관측값들로 연구자가 측정, 관찰한 결과들의 집합
일반적으로 시간적 공간적 제약으로 인해 모집단 전체를 분석하는 것을 불가능하여 표본을 통해 모집단의 특성을 이해함
모수 (parameter)
통계적 추론에서 연구자의 최종 목표, 모집단의 특성
통계량 (Statistic)
표본의 관측값들에 의해서 결정되는 양
- 대한민국 남자의 평균 키를 알아보기 위해 무작위로 대한민국 남자 100명을 선택해 그들의 키를 평균 내보았다.
- 모집단: 모든 대한민국 남성
- 표본: 대한민국 남자 100명
- 모수: 대한민국 남자의 평균 키 (모집단의 특성)
- 통계량: 표본 평균
자료의 종류
수치형
숫자로 이뤄진 자료
- 연속형(continuous data): 두 값 사이에 새로운 값이 존재할 수 있는 자료 (ex 몸무게, 키)
- 이산형(discrete data): 두 값 사이에 새로운 값이 존재할 수 없는 자료( ex 사람 수, 출산 횟수)
범주형(Categorical data)
n개의 범주로 나눠진 자료
- 순위형(ordinal data): 명목 척도를 가지지만 순서에 의미가 있는 척도 (ex 학점 등)
- 명목형(nominal data): 성별(남/여), 혈액형(A/B/O/AB) 등
자료의 수치
중심 경향값(대푯값)
전반적인 자료가 어디에 위치하는지 알아보기 위한 지표 (모집단의 요약값을 구체적으로 알아내기 위해서는 표본을 수치화시켜야 하기 때문)
- 평균(mean): 모든 자료를 더하고 자료의 크기로 나눈 값
- \( \mu = \frac{x_{1}+x_{2}+ \ldots +x_{N}}{N} = \frac{ \sum_{x=1}^N x_{i} }{N} \)
- 중앙값(median): 크기순으로 정럴시켰을때 중앙에 오는 값
- 최빈값(mode): 가장 빈도가 높은 값

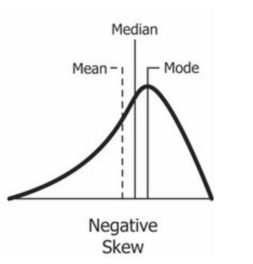
위의 그래프를 보면 평균과 중앙값이 같을 때는 그래프가 좌우 대칭일 때라는 걸 알 수 있다.
skew 그래프를 보았을 때 꼬리가 길어짐에 따라 평균이 따라가는 것을 보면 평균은 이상치에 영향을 많이 받고 중앙값을 평균에 비해 이상치의 영향을 덜 받는 것을 알 수 있다.
산포도
데이터의 퍼진 정도를 수치화한 것
- 분산(Variance): 데이터가 중심에서 떨어진 정도를 수치화한 것
- \( \sigma^{2}= \sum_{i=1}^N (x_{i}-\mu)^2 \)
- 사분위수: 전체 관측치를 크기순으로 정렬했을 때 일정한 범위로 4 분위로 나눈 값

정규분포
- 자연과학 현상을 설명할 때 가장 많이 쓰이는 분포로 대부분의 데이터는 정규분포 형태를 띠고 있음
- 중앙의 위치는 평균, 퍼진 정도는 분산에 의해 결정됨

왜도(Skewness)
- 분포의 비대칭 정도
- 꼬리가 긴 쪽의 방향으로 이름을 지음
- Negative skew = left skew
- positive skew = right skew

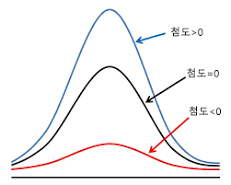
첨도(Kutosis)
분포 꼬리 부분의 두꺼움 정도
\( K_{s} = 0 \)이 크다면 그래프가 뾰족한 형태를 띠고 작다면 완만한 형태를 띰
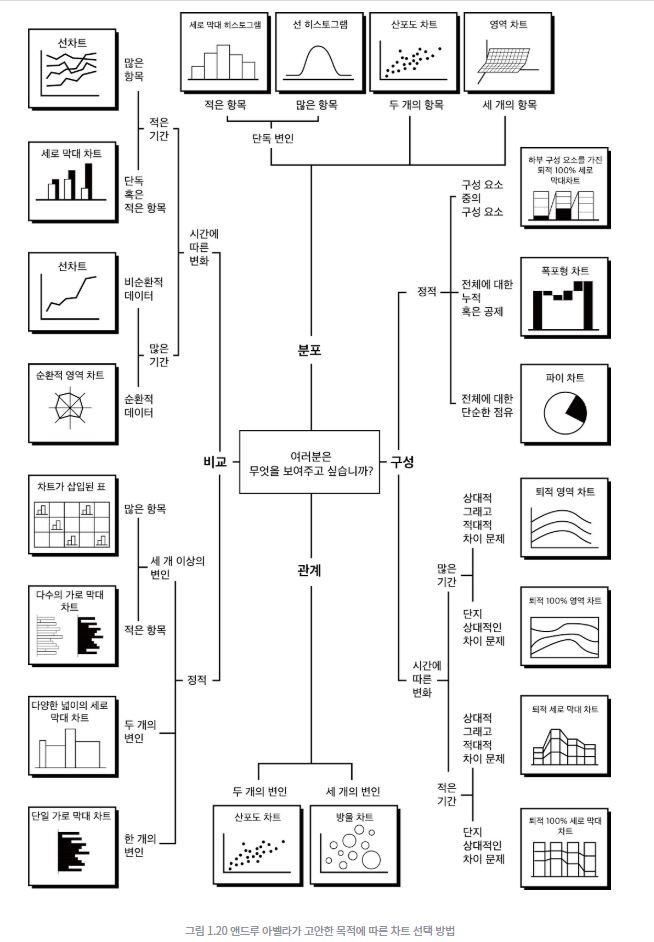
자료의 시각화
각 자료들은 쓰임에 따라 다양한 그래프를 사용하여 나타낼 수 있음

'Machine Learning > 기법' 카테고리의 다른 글
| [통계] 행렬(Matrix), 행렬 연산 (0) | 2023.03.23 |
|---|---|
| [통계] Likelihood, MLE, 가능도함수, 우도함수 (0) | 2023.03.21 |
| [ML] 머신러닝 Machine Learning 앙상블 Ensemble (0) | 2023.01.17 |
| [ML] 정규화 (0) | 2023.01.16 |
| [ML] Optimizer 옵티마이저, 최적화 (0) | 2023.01.13 |
통계학
산술적 방법을 기초로 하여, 주로 다량의 데이터를 관찰하고 정리 및 분석하는 방법을 연구하는 수학의 한 분야

모집단 (Population)
연구자가 알고 싶어 하는 대상이 되는 모든 개체들을 모은 집합 (집단 전체)
표본 (Sample)
모집단에서 측정한 일부분의 관측값들로 연구자가 측정, 관찰한 결과들의 집합
일반적으로 시간적 공간적 제약으로 인해 모집단 전체를 분석하는 것을 불가능하여 표본을 통해 모집단의 특성을 이해함
모수 (parameter)
통계적 추론에서 연구자의 최종 목표, 모집단의 특성
통계량 (Statistic)
표본의 관측값들에 의해서 결정되는 양
- 대한민국 남자의 평균 키를 알아보기 위해 무작위로 대한민국 남자 100명을 선택해 그들의 키를 평균 내보았다.
- 모집단: 모든 대한민국 남성
- 표본: 대한민국 남자 100명
- 모수: 대한민국 남자의 평균 키 (모집단의 특성)
- 통계량: 표본 평균
자료의 종류
수치형
숫자로 이뤄진 자료
- 연속형(continuous data): 두 값 사이에 새로운 값이 존재할 수 있는 자료 (ex 몸무게, 키)
- 이산형(discrete data): 두 값 사이에 새로운 값이 존재할 수 없는 자료( ex 사람 수, 출산 횟수)
범주형(Categorical data)
n개의 범주로 나눠진 자료
- 순위형(ordinal data): 명목 척도를 가지지만 순서에 의미가 있는 척도 (ex 학점 등)
- 명목형(nominal data): 성별(남/여), 혈액형(A/B/O/AB) 등
자료의 수치
중심 경향값(대푯값)
전반적인 자료가 어디에 위치하는지 알아보기 위한 지표 (모집단의 요약값을 구체적으로 알아내기 위해서는 표본을 수치화시켜야 하기 때문)
- 평균(mean): 모든 자료를 더하고 자료의 크기로 나눈 값
- μ=x1+x2+…+xNN=∑Nx=1xiN
- 중앙값(median): 크기순으로 정럴시켰을때 중앙에 오는 값
- 최빈값(mode): 가장 빈도가 높은 값

위의 그래프를 보면 평균과 중앙값이 같을 때는 그래프가 좌우 대칭일 때라는 걸 알 수 있다.
skew 그래프를 보았을 때 꼬리가 길어짐에 따라 평균이 따라가는 것을 보면 평균은 이상치에 영향을 많이 받고 중앙값을 평균에 비해 이상치의 영향을 덜 받는 것을 알 수 있다.
산포도
데이터의 퍼진 정도를 수치화한 것
- 분산(Variance): 데이터가 중심에서 떨어진 정도를 수치화한 것
- σ2=∑Ni=1(xi−μ)2
- 사분위수: 전체 관측치를 크기순으로 정렬했을 때 일정한 범위로 4 분위로 나눈 값

정규분포
- 자연과학 현상을 설명할 때 가장 많이 쓰이는 분포로 대부분의 데이터는 정규분포 형태를 띠고 있음
- 중앙의 위치는 평균, 퍼진 정도는 분산에 의해 결정됨

왜도(Skewness)
- 분포의 비대칭 정도
- 꼬리가 긴 쪽의 방향으로 이름을 지음
- Negative skew = left skew
- positive skew = right skew


첨도(Kutosis)
분포 꼬리 부분의 두꺼움 정도
Ks=0이 크다면 그래프가 뾰족한 형태를 띠고 작다면 완만한 형태를 띰

자료의 시각화
각 자료들은 쓰임에 따라 다양한 그래프를 사용하여 나타낼 수 있음


'Machine Learning > 기법' 카테고리의 다른 글
| [통계] 행렬(Matrix), 행렬 연산 (0) | 2023.03.23 |
|---|---|
| [통계] Likelihood, MLE, 가능도함수, 우도함수 (0) | 2023.03.21 |
| [ML] 머신러닝 Machine Learning 앙상블 Ensemble (0) | 2023.01.17 |
| [ML] 정규화 (0) | 2023.01.16 |
| [ML] Optimizer 옵티마이저, 최적화 (0) | 2023.01.13 |
