Likelihood(가능도함수, 우도함수)
데이터가 특정 분포로부터 만들어졌을 확률을 뜻한다.
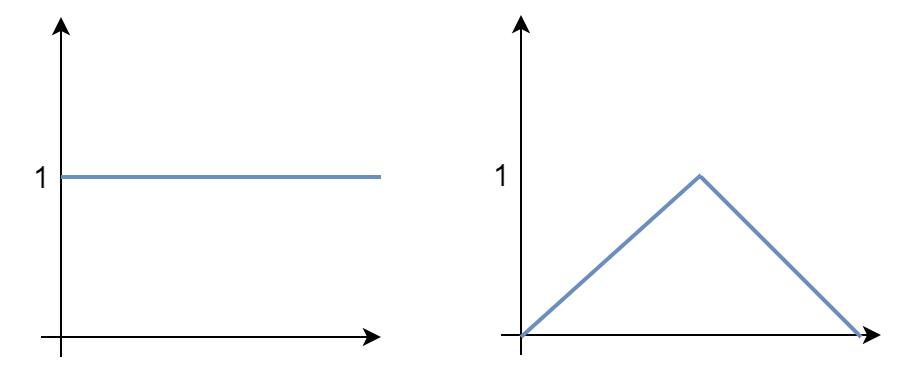
\( x = {1, 1, 1, 1} \)이라고 할 때 왼쪽의 분포를 따를 확률이 더 높고 아래와 같은 수식으로 적을 수 있다.
$$ L( \theta) = p(X \mid \theta) $$
\( \theta \)의 파라미터를 가지는 분포
계산
$$ p(x_{n} \mid \theta)= \frac{1}{ \sqrt{2 \pi} \sigma }exp\{ - \frac{(x_{n}- \mu)^{2}}{2 \sigma ^{2}} \} $$
\( x_{n} \)이 \( \theta = ( \mu, \sigma) \)를 가지는 정규분포를 따를 확률
모든 데이터는 독립이기 때문에 그것을 적용하면 아래와 같은 likelihood 식을 얻을 수 있다.
$$ L(\theta)=p(X \mid \theta)= \prod_{n=1}^N p(x_{n}, \theta) $$
확률분포함수와 개념적으로 반대되는 지표로 같은 식에 대해 변수를 다른 관점에서 봄
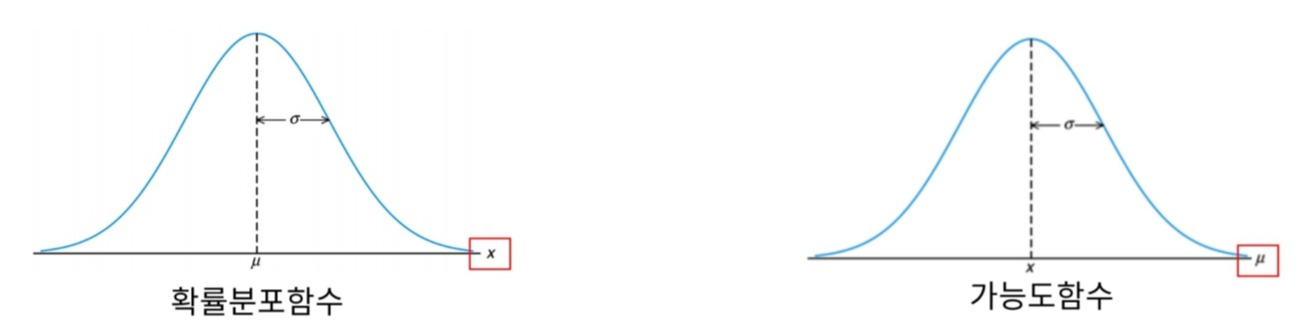
- 확률분포함수
- x값에 대한 \( \mu \)의 함수
- 모수를 알 때, 확률변수의 실현값을 예측하고자 함
- 평균이 2일 때, 새로운 x의 값을 몇일까?
- 가능도함수
- \( \mu \)에 대한 x의 함수
- 확률변수 실현값을 알 때, 모수를 추정하고자 함
- x1 = 1, x2 = 3, x3 = 3일 때, 평균은 몇일까?
확률분포함수(Probability Distriburion Function)
- 확률밀도함수(PDF:Probability Density Function)
- 연속형 확률변수의 확률분포함수
- 확률질량함수(PMF:Probability mass Function)
- 이산형 확률변수의 확률분포함수
- 누적분포함수(CDF:Cumulative Distribution Function)
- 누적확률분포함수
주로 likelihood에서 쓰는 분포함수는 확률밀도함수, 확률질량함수이다.
\( \mu \) 추정
\( x_{1},x_{2},x_{3} \) 변수가 있다고 할 때, \( \mu \)에 따라 달리지는 그래프 (정규분포식에 대입함, 분모에 곱해지는 1은 분산임)
$$ f(x_{1},x_{2},x_{3}) = ( \frac{1}{ \sqrt{2 \pi \cdot 1}} )^{3}exp( -\frac{(x_{1}-\mu_{0})^{2}(x_{2}-\mu_{0})^{2}(x_{3}-\mu_{0})^{2}}{2 \cdot1} ) $$
Probabilitu Density Function
평균 \( \mu \), 분산 1의 독립정규분포를 따르는 확률변수 \( X_{i} \)의 확률분포함수
$$ f(x_{i})= \frac{1}{ \sqrt{2\pi \cdot 1}}exp(- \frac{(x_{i}-\mu_{0})^{2}}{2 \cdot1}) $$
\( X_{1} \) = \(x_{1}\),\( X_{2} \) = \(x_{2}\), 2개의 자료가 있을 때, 확률분포함수
$$ f(x_{1},x_{2})= (\frac{1}{ \sqrt{2\pi \cdot 1}})^{2}exp(- \frac{(x_{1}-\mu_{0})^{2}(x_{2}-\mu_{0})^{2}}{2 \cdot1}) $$
Likelihood Function
위와 동일한 함수식에 변수만 \( \mu_{0}\)로 바꿈
$$ L(\mu_{0};x_{1},x_{2})=( \frac{1}{ \sqrt{2\pi \cdot 1}} )^{2}exp(- \frac{(\mu_{0}-x_{1})^{2}(\mu_{0}-x_{2})^{2}}{2\cdot1}) $$
자료가 2개 있을 때 \( mu \)에 관한 함수는 L이다.라는 뜻
그리고 이 함수를 크게 만드는 \( mu \)를 평균으로 추정할 수 있음
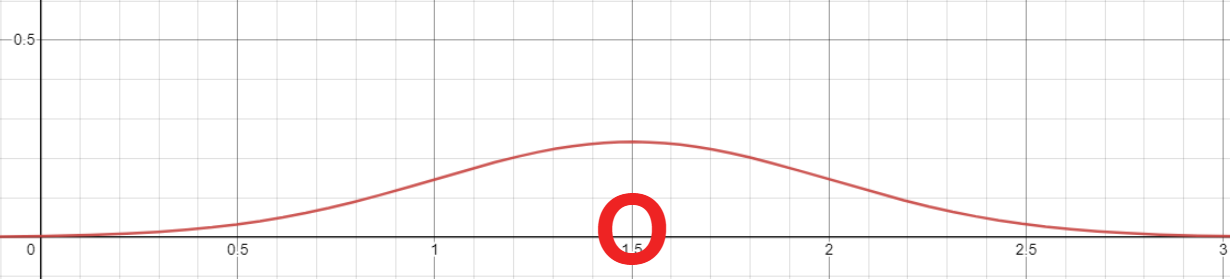
x가 1, 2라는 값을 가지고 있을 때 Likelihood Function
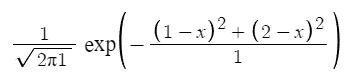
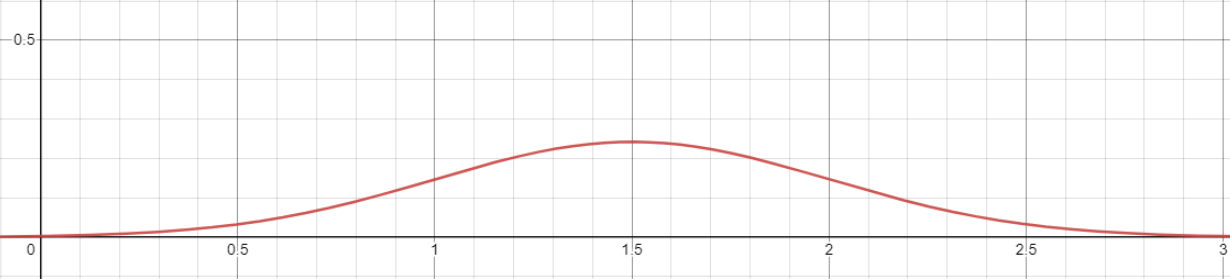
- 여기서 1.5가 1, 2의 평균이 될 확률이 높다는 것을 알 수 있음
- likelihood를 최대로 만드는 모수의 값을 MLE(Maximum Likelihood Estimator)라고 함
- MLE는 미분을 통해 구할 수 있음
MLE(Maximum Likelihood Estimator)
likelihood를 최대화하는 \( \theta \)를 찾을 때 사용한다.
Likelihood는 \( mu \)에 대한 함수였다면 MLE는 \( \hat{\mu} \)로 likelihood를 \( \mu \)로 미분했을 때 0이 되게 만드는 값이다.
MLE 계산
Likelihood
$$ L(\mu_{0};x_{1},x_{2})=( \frac{1}{ \sqrt{2\pi \cdot 1}} )^{2}exp(- \frac{(\mu_{0}-x_{1})^{2}(\mu_{0}-x_{2})^{2}}{2\cdot1}) $$
log 재구성
$$ E( \theta) = -ln L(\theta)=-\sum_{n=1}^N lnp(x_{n} \mid \theta) $$
미분하기 편하게 log를 사용하여 Likelihood를 재구성함
- log는 단조증가함수이기 때문에 Likelihood가 제일 큰 값을 가질때 log도 제일 큰 값을 가짐
- log와 exp는 서로 역함수 관계이기 때문에 상쇄되어 상수만 나옴
$$ logL(\mu_{0};1,2) = - \frac{2}{2}log(2\pi) - \frac{1}{2}((\mu_{0}-1)^{2}+(\mu_{0}-2)^{2}) $$
미분
$$ \frac{ \delta logL(\mu_{0};1,2)}{ \delta \mu_{0}}=- \frac{1}{2}(2(\mu_{0}-1)+2(\mu_{0}-2)) $$
미분 값이 0이 되게 하는 표본평균 \( \hat{\mu_{0}} \) 구하기 = MLE
$$ - \frac{1}{2}(2(\mu_{0}-1)+2(\mu_{0}-2)) = 0 $$
$$ 2\mu_{0} = 3 $$
$$ \mu_{0} = \frac{3}{2} $$
모집단의 모수를 추정하기 위해 Likelihood를 사용하고 MLE가 추정값이 된다.
MLE는 미분을 통해 구할 수 있다.
'Machine Learning > 기법' 카테고리의 다른 글
| [통계] 행렬(Matrix), 행렬 미분 (0) | 2023.03.30 |
|---|---|
| [통계] 행렬(Matrix), 행렬 연산 (0) | 2023.03.23 |
| [통계] 통계 기초 (0) | 2023.03.16 |
| [ML] 머신러닝 Machine Learning 앙상블 Ensemble (0) | 2023.01.17 |
| [ML] 정규화 (0) | 2023.01.16 |
