Seq2seq

seq2seq 모델은 인코더 디코더 구조를 사용하고 RNN보다 번역 성능에서 우수한 성능을 보여주었다.
그러나 입력 시퀀스를 하나의 고정된 크기의 벡터로 압축하면서 정보손실이 발생한다는 한계점이 존재한다. 더 자세히는 encoder의 마지막 노드에서 나온 시퀀스를 decoder에서 받기 때문에 정보의 손실이 일어날 수밖에 없다.
Attention
encoder에 매 time step으로부터 하나씩 벡터 표현을 추출하면서, 중요한 단어에 집중할 수 있도록 설계된 것이다.
모든 기억을 동등하게 기억하지 않고 연관성 있는 기억에 집중해서 기억하도록 구조화하는 방법을 사용함

출력 단어를 예측하는 시점에서 예측할 단어와 연관이 큰 단어를 더 집중해서 참고하는 모습을 볼 수 있다.
역할
encoder와 decoder 사이의 인터페이스로 모든 encoder의 은닉상태의 정보를 decoder에 전달하며 이러한 구조를 가지게 되면 모델이 선택적으로 입력 시퀀스의 유용한 부분에 집중할 수 있다.
추가적으로 encoder와 decoder의 alignment를 학습하게 됨
alignment: 번역 전 텍스트 부분을 번역 후 텍스트 부분과 연결하는 것

사용하는 이유
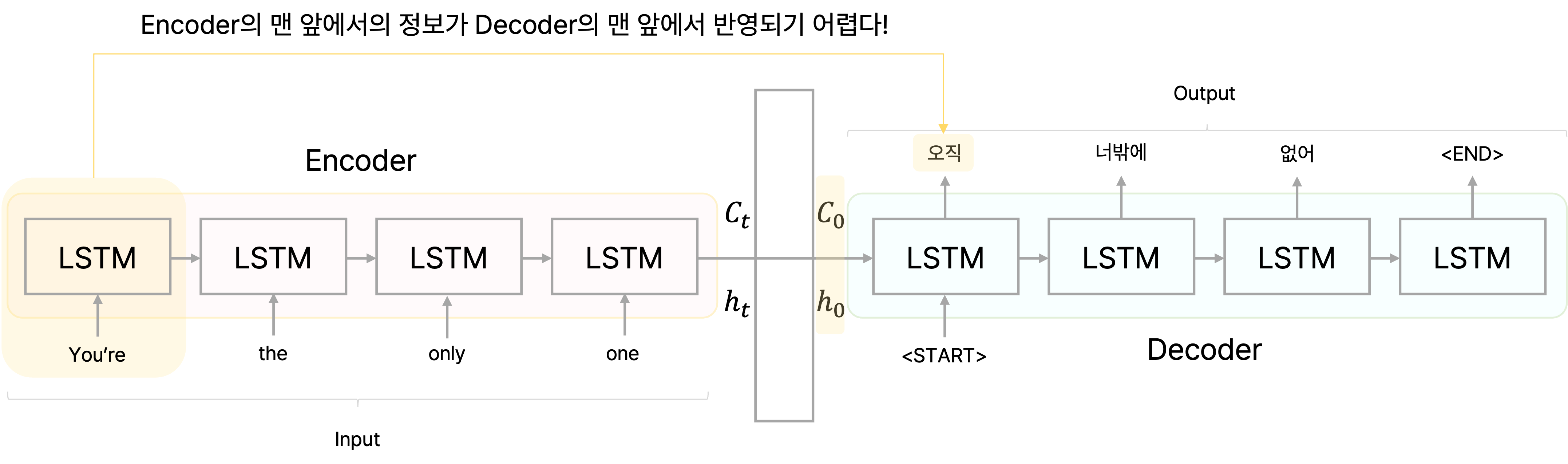
앞에서 설명한 seq2seq의 단점 때문이다. encoder 마지막 time step에서 내보내는 hidden state에 모든 문장 정보가 담기고 이 메모리는 유한하기 때문에 정보 소실이 생길 수밖에 없다.
이로 인해 encoder의 hidden state는 입력 문장 맨 앞의 주어 정보를 갖지 못할 가능성이 생긴다.
Seq 2 Seq with Attention
구조
각 decoder time step에서 attention을 진행하여 연관 있는 input의 가중치를 더한다.

Notation
Attention은 Encdoer의 모든 Hidden_state 중에서 어디에 집중할지를 Query, Key, Value를 통해 구한다.
Query: 현재 time-step의 decoder output
Key: 각 time-step 별 endcoder output
Values: 각 time-step 별 encoder output
영어를 독일어로 번역할 때 Attension을 쓰지 않으면 영어 문장을 다 읽고 , 단어를 하나씩 독일어로 번역해야 하며 이때 문장이 길다면 앞의 내용을 까먹을 것이다.
Attention을 쓴다면 영어 문장을 다 읽고 키워드를 활용하여 독일어로 번역한다.
계산

디코더의 3번째 cell의 예측값을 구하는 과정을 알아보자.
먼저 3번째 cell을 예측하기 위해서 Attention Score가 필요하고 Softmax를 하면 위의 사진처럼 나타낼 수 있다.
Softmax값을 통해 l, am, a, student 단어 각각이 출력 단어 예측에 얼마나 도움이 되는지를 확인할 수 있다.
Attention Score를 구하는 과정은 아래와 같다
Step 1
Attention Score를 구한다.

인코더의 시점을 각 1, 2, ..., N이라고 하면 인코더의 은닉 상태는 \( h_{1}, h_{2}, ...,h_{N} \)라고 정의한다.
디코더의 현재 시점 t에서의 디코더의 은닉 상태는 \( s_{t} \)라고 정의한다.
t를 예측하기 위해서는 \( h_{t-1} \)과 이전 출력단어가 필요하며 여기에 attention이 적용되면 \( a_{t} \)라는 어텐션 값이 추가로 더 필요하다.
\( a_{t} \)란 디코더의 step t의 단어를 예측하기 위해, 인코더의 모든 은닉 상태 각각이 디코더의 현 은닉상태 \( s_{t} \)와 얼마나 유사한지 판단하는 점수이다.

\( s_{t}^{T} \)와 각 은닉 상태와 내적을 수행하여 \( s_{t} \)와 인코더 i번째 은닉 상태의 어텐션 스코어를 계산한다.
$$ score(s_{t}, h_{i})=s_{t}^{T}h_{i} $$
모든 인코더의 은닉상태의 score를 구하면 아래와 같이 쓸 수 있다. -> \( e^{t} \)로 정의하겠음
$$ e^{t}=[s_{t}^{T}h_{1},...,s_{t}^{T}h_{N}] $$
Step 2
softmax를 통해 어텐션 분포를 구한다.

앞에서 구했던 \( e^{t} \)에 softmax를 적용된 각각의 값을 Attention Weight라고 한다. (Attention Weight의 수식은 \( \alpha^{t } \))
$$ \alpha^{t } = softmax(e^{t}) $$
Step 3
각 인코더의 Attention weight와 은닉상태를 가중합 하여 Attention Value 구하기

$$ a_{t} = \sum_{i=1}^N \alpha_{i}^{t} h_{i} $$
어텐션 값은(\( a_{t}\)) 인코더의 문맥을 포함하고 있다고 하여 Context vector라고도 불림
자세한 계산
어텐션을 계산하기 위해서는 key, value로 이뤄진 목록과 쿼리 q가 정의되어야 한다. 쿼리 q를 기준으로 각 key 와의 연관 정도를 계산하며, 그에 비려해서 키에 대응하는 값 value를 어텐션 값으로 사용한다.
$$ key-value (k_{i},v_{i}),i=1,2, \cdots , N $$
$$ attention(q,k,v) $$

계산 순서

1. 쿼리 q와 \( (k_{i}, v_{i}) \)목록의 각 \( k_{i} \)와 attention score를 계산한다.
2. 쿼리 q와 키 \( k_{i} \)의 연관 정도를 어텐션 점수로 환산한다.
3. 계산된 어텐션 점수와 값\( v_{i} \)를 곱해서 모두 합산하거나 가장 큰 어텐션 점수와 대응하는 \( v_{i} \)를 곱해서 최종 어텐션으로 사용한다.
$$ score(q,k)= \frac{q^{T}k}{ \sqrt{n}} $$
$$ softmax(score(q,k)) $$
어텐션 점수는 내적을 이용하여 계산하고 q, k의 크기가 달라져도 동일한 내적값을 얻기 위해 q, k의 벡터 크기인 \( \sqrt{n} \)으로 나눠서 정규화한다. 종종 softmax를 사용하여 확률로 변환시키기도 한다.

일괄처리



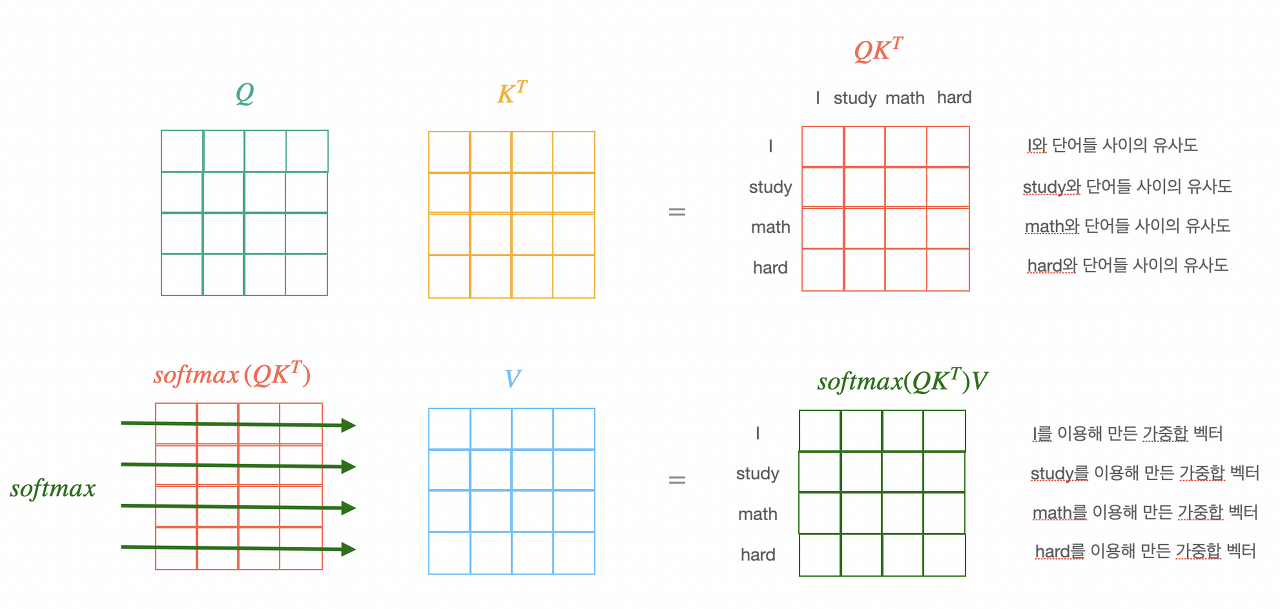
인코더 디코더

기계 번역을 위한 순환 신경망 인코더-디코더 모델에 어텐션을 적용해 보자.
인코더는 한 문장을 입력받아서 마지막 상태인 context를 디코더에 전달하고, 디코더를 받은 context를 이용해서 다른 언어로 된 문장을 생성한다. 이러한 구조는 입력 문장이 길어질수록 오래전에 입력된 단어를 잘 기억하지 못한다는 단점을 가지고 있다.
어텐션 접목
context 벡터 생성 시에 어텐션을 접목시켜 디코더가 새로운 단어를 생성할 때 입력 문장에서 연관된 단어 정보를 가져오게 한다. 이를 위해서는 인코더의 모든 은닉 상태와 어텐션을 계산해야 한다.

어텐션 계산
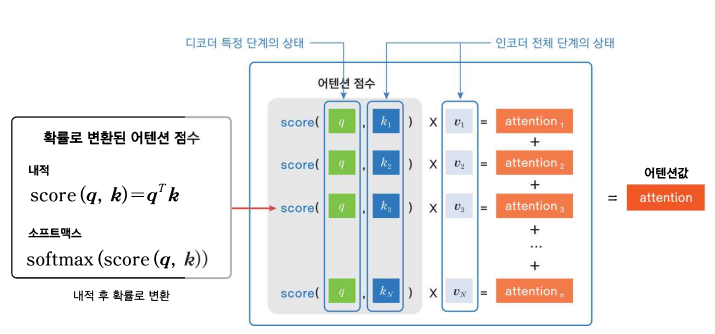
디코더 첫 번째 은닉상태가 쿼리 q가 되고 이에 대한 attention score는 hello와 연관이 있을수록 높게 나온다. 어텐션 점수를 가중치로 하여 인코더의 모든 상태와 가중합산한 값을 최종 어텐션 값으로 사용하고 이는 디코더에 전달되며 디코더의 현태 은닉상태와 합쳐져서 출력 계층에 전달된다.
'NLP' 카테고리의 다른 글
| [NLP] 자연어처리의 이해 (0) | 2023.04.03 |
|---|---|
| [RNN] Transformer (0) | 2023.01.31 |
| [RNN] Backpropagation through time (0) | 2023.01.30 |
| [RNN] RNN 모델 종류 (0) | 2023.01.26 |
| [RNN] RNN 구조 (0) | 2023.01.26 |
Seq2seq

seq2seq 모델은 인코더 디코더 구조를 사용하고 RNN보다 번역 성능에서 우수한 성능을 보여주었다.
그러나 입력 시퀀스를 하나의 고정된 크기의 벡터로 압축하면서 정보손실이 발생한다는 한계점이 존재한다. 더 자세히는 encoder의 마지막 노드에서 나온 시퀀스를 decoder에서 받기 때문에 정보의 손실이 일어날 수밖에 없다.
Attention
encoder에 매 time step으로부터 하나씩 벡터 표현을 추출하면서, 중요한 단어에 집중할 수 있도록 설계된 것이다.
모든 기억을 동등하게 기억하지 않고 연관성 있는 기억에 집중해서 기억하도록 구조화하는 방법을 사용함

출력 단어를 예측하는 시점에서 예측할 단어와 연관이 큰 단어를 더 집중해서 참고하는 모습을 볼 수 있다.
역할
encoder와 decoder 사이의 인터페이스로 모든 encoder의 은닉상태의 정보를 decoder에 전달하며 이러한 구조를 가지게 되면 모델이 선택적으로 입력 시퀀스의 유용한 부분에 집중할 수 있다.
추가적으로 encoder와 decoder의 alignment를 학습하게 됨
alignment: 번역 전 텍스트 부분을 번역 후 텍스트 부분과 연결하는 것

사용하는 이유

앞에서 설명한 seq2seq의 단점 때문이다. encoder 마지막 time step에서 내보내는 hidden state에 모든 문장 정보가 담기고 이 메모리는 유한하기 때문에 정보 소실이 생길 수밖에 없다.
이로 인해 encoder의 hidden state는 입력 문장 맨 앞의 주어 정보를 갖지 못할 가능성이 생긴다.
Seq 2 Seq with Attention
구조
각 decoder time step에서 attention을 진행하여 연관 있는 input의 가중치를 더한다.

Notation
Attention은 Encdoer의 모든 Hidden_state 중에서 어디에 집중할지를 Query, Key, Value를 통해 구한다.
Query: 현재 time-step의 decoder output
Key: 각 time-step 별 endcoder output
Values: 각 time-step 별 encoder output
영어를 독일어로 번역할 때 Attension을 쓰지 않으면 영어 문장을 다 읽고 , 단어를 하나씩 독일어로 번역해야 하며 이때 문장이 길다면 앞의 내용을 까먹을 것이다.
Attention을 쓴다면 영어 문장을 다 읽고 키워드를 활용하여 독일어로 번역한다.
계산

디코더의 3번째 cell의 예측값을 구하는 과정을 알아보자.
먼저 3번째 cell을 예측하기 위해서 Attention Score가 필요하고 Softmax를 하면 위의 사진처럼 나타낼 수 있다.
Softmax값을 통해 l, am, a, student 단어 각각이 출력 단어 예측에 얼마나 도움이 되는지를 확인할 수 있다.
Attention Score를 구하는 과정은 아래와 같다
Step 1
Attention Score를 구한다.

인코더의 시점을 각 1, 2, ..., N이라고 하면 인코더의 은닉 상태는 \( h_{1}, h_{2}, ...,h_{N} \)라고 정의한다.
디코더의 현재 시점 t에서의 디코더의 은닉 상태는 \( s_{t} \)라고 정의한다.
t를 예측하기 위해서는 \( h_{t-1} \)과 이전 출력단어가 필요하며 여기에 attention이 적용되면 \( a_{t} \)라는 어텐션 값이 추가로 더 필요하다.
\( a_{t} \)란 디코더의 step t의 단어를 예측하기 위해, 인코더의 모든 은닉 상태 각각이 디코더의 현 은닉상태 \( s_{t} \)와 얼마나 유사한지 판단하는 점수이다.

\( s_{t}^{T} \)와 각 은닉 상태와 내적을 수행하여 \( s_{t} \)와 인코더 i번째 은닉 상태의 어텐션 스코어를 계산한다.
$$ score(s_{t}, h_{i})=s_{t}^{T}h_{i} $$
모든 인코더의 은닉상태의 score를 구하면 아래와 같이 쓸 수 있다. -> \( e^{t} \)로 정의하겠음
$$ e^{t}=[s_{t}^{T}h_{1},...,s_{t}^{T}h_{N}] $$
Step 2
softmax를 통해 어텐션 분포를 구한다.

앞에서 구했던 \( e^{t} \)에 softmax를 적용된 각각의 값을 Attention Weight라고 한다. (Attention Weight의 수식은 \( \alpha^{t } \))
$$ \alpha^{t } = softmax(e^{t}) $$
Step 3
각 인코더의 Attention weight와 은닉상태를 가중합 하여 Attention Value 구하기

$$ a_{t} = \sum_{i=1}^N \alpha_{i}^{t} h_{i} $$
어텐션 값은(\( a_{t}\)) 인코더의 문맥을 포함하고 있다고 하여 Context vector라고도 불림
자세한 계산
어텐션을 계산하기 위해서는 key, value로 이뤄진 목록과 쿼리 q가 정의되어야 한다. 쿼리 q를 기준으로 각 key 와의 연관 정도를 계산하며, 그에 비려해서 키에 대응하는 값 value를 어텐션 값으로 사용한다.
$$ key-value (k_{i},v_{i}),i=1,2, \cdots , N $$
$$ attention(q,k,v) $$

계산 순서

1. 쿼리 q와 \( (k_{i}, v_{i}) \)목록의 각 \( k_{i} \)와 attention score를 계산한다.
2. 쿼리 q와 키 \( k_{i} \)의 연관 정도를 어텐션 점수로 환산한다.
3. 계산된 어텐션 점수와 값\( v_{i} \)를 곱해서 모두 합산하거나 가장 큰 어텐션 점수와 대응하는 \( v_{i} \)를 곱해서 최종 어텐션으로 사용한다.
$$ score(q,k)= \frac{q^{T}k}{ \sqrt{n}} $$
$$ softmax(score(q,k)) $$
어텐션 점수는 내적을 이용하여 계산하고 q, k의 크기가 달라져도 동일한 내적값을 얻기 위해 q, k의 벡터 크기인 \( \sqrt{n} \)으로 나눠서 정규화한다. 종종 softmax를 사용하여 확률로 변환시키기도 한다.

일괄처리




인코더 디코더

기계 번역을 위한 순환 신경망 인코더-디코더 모델에 어텐션을 적용해 보자.
인코더는 한 문장을 입력받아서 마지막 상태인 context를 디코더에 전달하고, 디코더를 받은 context를 이용해서 다른 언어로 된 문장을 생성한다. 이러한 구조는 입력 문장이 길어질수록 오래전에 입력된 단어를 잘 기억하지 못한다는 단점을 가지고 있다.
어텐션 접목
context 벡터 생성 시에 어텐션을 접목시켜 디코더가 새로운 단어를 생성할 때 입력 문장에서 연관된 단어 정보를 가져오게 한다. 이를 위해서는 인코더의 모든 은닉 상태와 어텐션을 계산해야 한다.

어텐션 계산

디코더 첫 번째 은닉상태가 쿼리 q가 되고 이에 대한 attention score는 hello와 연관이 있을수록 높게 나온다. 어텐션 점수를 가중치로 하여 인코더의 모든 상태와 가중합산한 값을 최종 어텐션 값으로 사용하고 이는 디코더에 전달되며 디코더의 현태 은닉상태와 합쳐져서 출력 계층에 전달된다.
'NLP' 카테고리의 다른 글
| [NLP] 자연어처리의 이해 (0) | 2023.04.03 |
|---|---|
| [RNN] Transformer (0) | 2023.01.31 |
| [RNN] Backpropagation through time (0) | 2023.01.30 |
| [RNN] RNN 모델 종류 (0) | 2023.01.26 |
| [RNN] RNN 구조 (0) | 2023.01.26 |
