순차 데이터
순차 데이터(sequence data)란 시간적 공간적 순서 관계가 있는 데이터이다. 자연 현상과 음악, 동영상, 주가, 시스템로그, 글, 악보, 프로그램과 같이 구성요소가 순차적인 관계를 가지고 있다.
시간 정보를 포함한 데이터를 FNN과 CNN으로 처리를 하였을 때 과연 좋은 결과를 얻을 수 있을까?
FNN을 사용하면 고정된 입력크기를 사용하기 때문에 가변 길이를 가지는 데이터를 사용하지 못하고 CNN은 이미지 저리를 위해 만들어졌기 때문에 순차적 관계를 알아낼 수 없다.
RNN 구조
RNN(Recurrent neural network)는 데이터의 순서를 고려하는 context를 만들어 데이터의 순차 구조를 인숙할 수 있고 context의 번위가 넓더라도 처리할 수 있다.

순차 구조를 인식하기 위래 데이터를 시간의 순서에 맞게 하나씩 입력 받고 은닉 계층에서 피드백 연결을 가진다.
기본적으로 입력 계층, 은닉 계층, 출력 계층으로 이루어지며 은닉 계층은 여러 계층이 될 수 있지만 계층을 깊게 쌓아도 성능이 향상되지 않는 경우가 일반적이기 때문에 일반적으로 한 두 층의 계층으로 설계한다.
입력 계층, 은닉 계층, 출력 계층 순서대로 실행되나 은닉 계층에 피드백 연결이 있기 때문에 은닉 상태가 다음 단계로 전달된다는 차이점이 있다.
이때 은닉 계층에는 시간 단계별로 입력된 데이터가 순차적으로 추상화하여 형성된 context를 담고 있다 따라서 피드백 연결은 시간의 흐름에 따라 context를 기억하는 과정으로 생각할 수 있다.
순환 연결 방식
초기 은닉 상태 \( h_{o} \)은 영벡터로 가정하고 각 단계를 변수 \( t \)로 표현하면 아래와 같은 순서로 실행된다.
- 입력 게층은 새로운 입력 데이터 \( x_{1} \)를 입력받는다.
- 은닉 계층은 다음 순서로 실행된다
- 이전 상태 \( h_{t-1} \)와 입력 데이터 \( x_{1} \)를 합쳐서 \( (h_{t-1}, x_{t}) \)로 입력받는다.
- 함수 \( f_{w}(h_{t-1}, x_{t}) \) 를 실행해서 은닉 상태 \( h_{t} \)를 출력한다.
- 함수 \( f_{w} \)는 순환 신경망의 종류에 따라 달라지며 \( W \)는 은닉 계층의 가중치를 나타낸다.
- 은닉 상태 \( h_{t} \)는 출력 계층과 다음 단계의 은닉 계층에 전달된다.
- 출력 계층은 은닉 상태 \( h_{t} \)를 입력받아서 뉴런 연산 후 \( y_{1} \)를 출력한다.
이때 \( f_{w} \)가 다음과 같은 형태로 정의되는 신경망을 기본 순환 신경망(Vanila RNN) 이라고 한다.
$$ \begin{align*} h_{1} = tanh(W_{hh}h_{t-1}+W_{xh}x_{t})\\ = tanh((W_{hh}W_{xh})\binom{h_{t-1}}{x_{t}})\\ = tanh(W\binom{h_{t-1}}{x_{t}}), W=(W_{hh}, W_{xh}) \end{align*} $$

- \( W_{xh} \): 입력 계층과 은닉 계층을 연결하는 가중치
- \( W_{hh} \): 은닉 계층의 피드백 연결에 대한 가중치
- \( W_{hy} \): 은닉 계층과 출력 계층을 연결하는 가중치
입력 은닉

은닉 상태는 지금까지 입력된 모든 데이터가 추상화되어 있다는 것을 알 수 있다. 이를 점화식으로 나타내면 아래의 식과 같다.
$$ h_{t}=f_{w}(h_{t-1}, x_{t}) $$
위의 식을 전개해 보면 아래와 같이 쓸 수 있다.
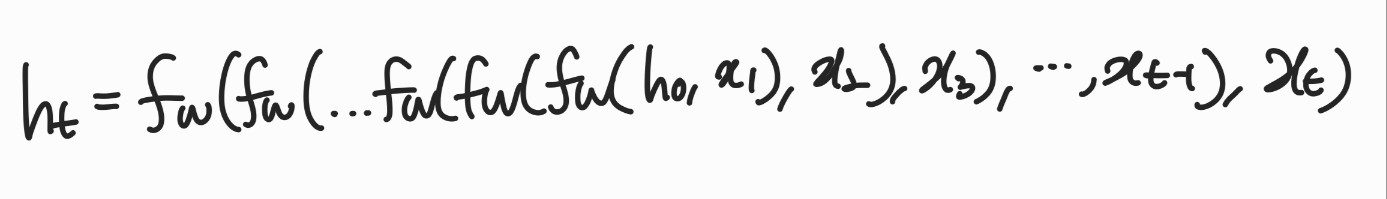
출력
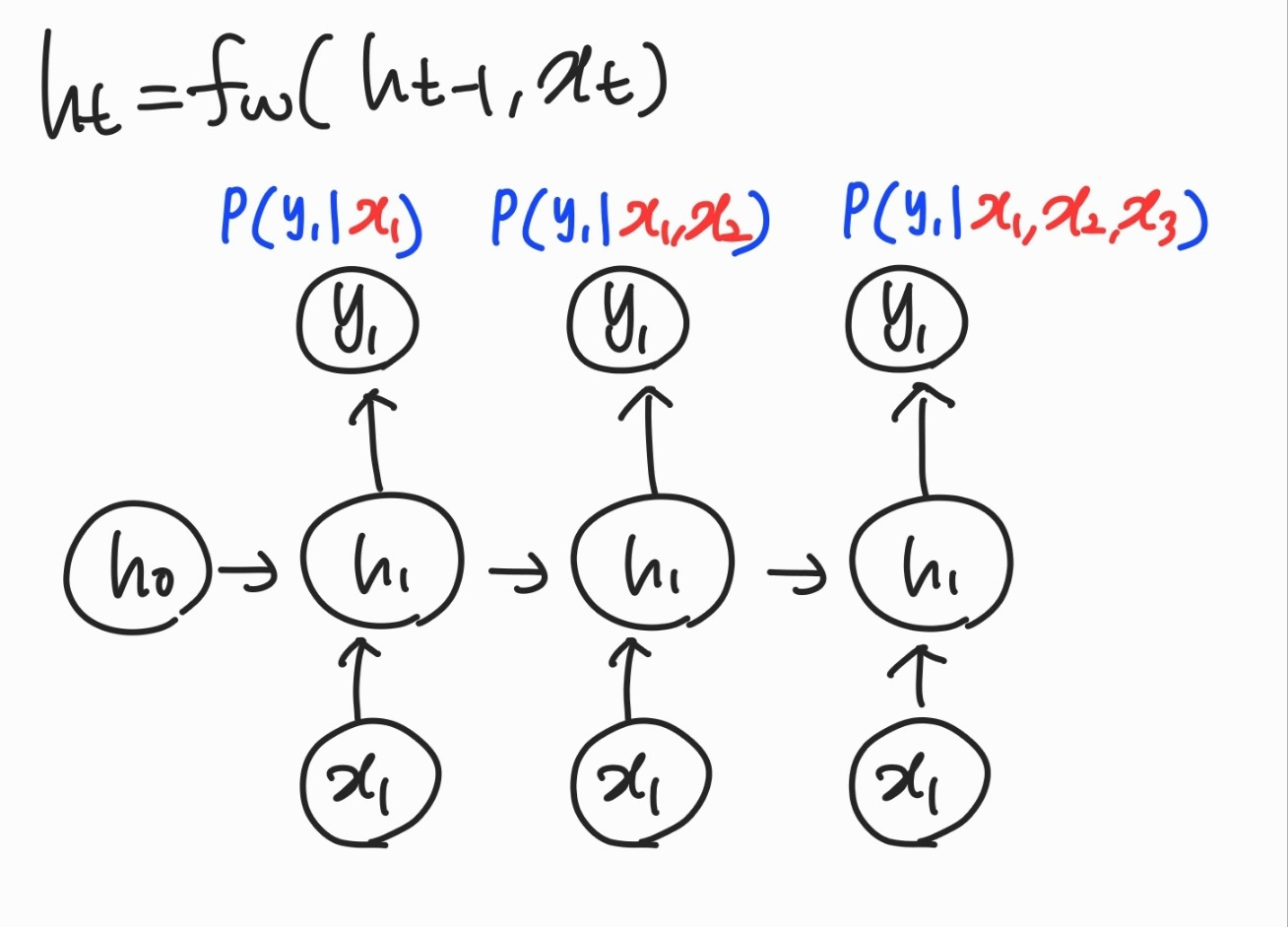
출력은 입력에 대한 조건부 확률을 표현하고 조건부 식은 각 계층마다 위와 같다.
가중치 공유
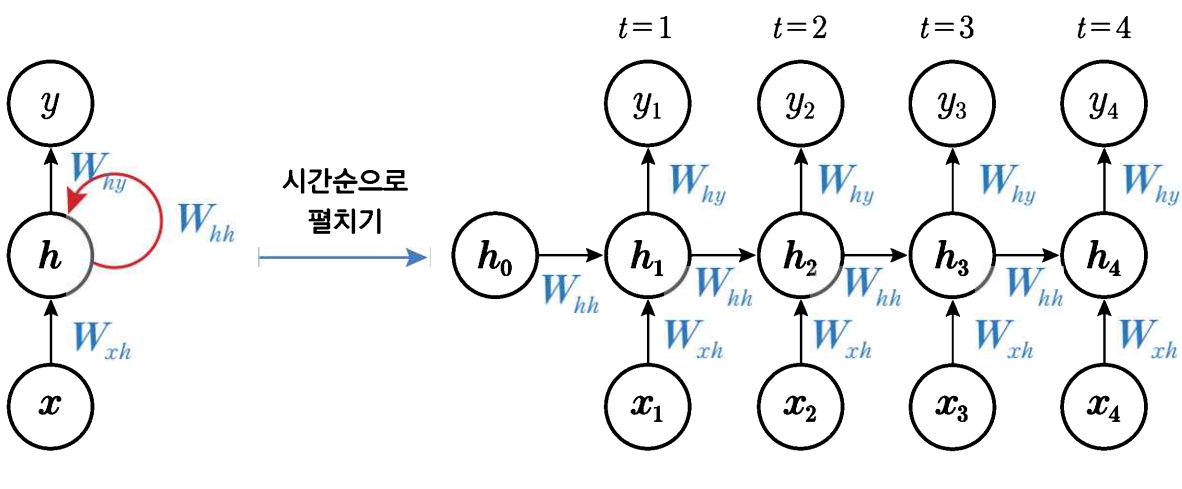
- 순차 구조를 포착할 수 있다.
- 데이터의 다양한 순차 구조를 하나의 가중치로 학습시키기 때문에 어느 위치에 나타나더라도 포착할 수 있음
- 가변 길이 데이터를 처리하기 쉽다.
- 모든 단계가 같은 파라미터를 사용하므로 단계를 쉽게 추가할 수 있다
- 파라미터 수가 절약되고 정규화 효과가 생긴다
- 파라미터를 공유하면 파라미터 수가 줄고 비슷한 유형의 순차 패턴에 대해 일반화를 잘할 수 있다.
'NLP' 카테고리의 다른 글
| [NLP] 자연어처리의 이해 (0) | 2023.04.03 |
|---|---|
| [RNN] Transformer (0) | 2023.01.31 |
| [NLP] Seq2Seq with Attention (0) | 2023.01.31 |
| [RNN] Backpropagation through time (0) | 2023.01.30 |
| [RNN] RNN 모델 종류 (0) | 2023.01.26 |
