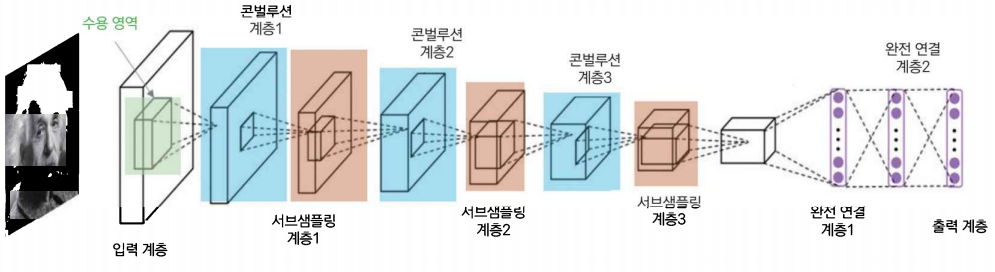
convolution layer와 Subsampling layer로 이루어져 있다.
convolution 연산을 통해 이미지의 다양한 특징을 학습하며 Subsampling의 pooling을 통해 이미지의 크기를 줄이고 위치불변성을 갖도록 한다.
Convolution 연산
두 함수를 곱해 적분하는 연산으로 함수 \( f \)에 다른 함수 \( g \)를 적용하여 새로운 함수를 만들 때 사용한다.
$$ (f*g)=\int_{-\infty}^{\infty}f(\tau)g(t-\tau)d\tau $$
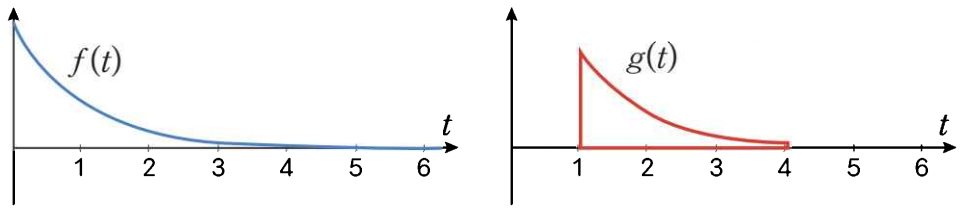
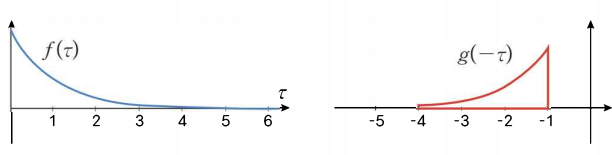

\( g(t- \tau) \) 함수만 \( t \)를 가지고 있어 움직일 수 있고 이를 그림으로 표현하면 위와 같고 \( t \)를 따라 슬라이딩하며 내적 한다.
Cross correlation 연산
두 함수의 유사도를 측정하는 방법이다.
$$ (f*g)=\int_{-\infty}^{\infty}f(\tau)g(t+\tau)d\tau $$
\( g( \tau) \)를 반전시키지 않고 사용하며 이것을 제외한 다른 것은 Convolution 연산과 같다.
이미지 특징 추출
Convolution 연산을 이미지에 입히면 경계선 검출(edge detection), 스무딩(smoothing), 샤프닝(sharpening)과 같은 특징을 추출을 할 수 있다.
https://pasongsong.tistory.com/178
[CNN] CNN 필터 filter (Convolutional Neural Network)
Computer Vision 시각적 세계를 이해하고 해석하는 학습을 하는 인공지능 분야 Kinds of Problems Image classification : image를 보고 분류하는 것 Object detection : 특정 object를 찾아내는 것 Nerual Style Transfer : image
pasongsong.tistory.com
2차원 이미지가 \( I \)이고 convolution filter가 \( K \)라면 이미지에 대한 convolution 연산 \( (I*K)(i,j) \)는 아래와 같이 정의된다.
$$ (I*K)(i,j)=\sum_{m} \sum_{n}I(m,n)K(i-m,j-n) $$
\( (i,j) \)는 픽셀 인덱스이며 이미지는 입력 함수가 되고 convolution filter는 가중치 함수가 되어 픽셀 단위로 가중합산을 한다.
이미지 처리를 할 때는 필터를 반전시키지 않기 때문에 교차 상관 연산을 하고 이는 아래와 같이 정의된다.
$$ (I*K)(i,j)=\sum_{m} \sum_{n}K(i+m, j+n) $$
convolution network는 교차 상관 연산을 하지만 convolution연산을 한다고 말하며 이는 2개의 성능적 차이는 없고 교차 상관 연산의 계산이 더 간단하기 때문이다.
이미지 연산
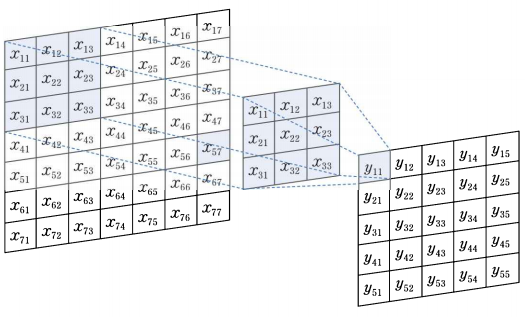
첫 번째 가중 합산
$$ \begin{align*} y_{11}= w_{11}x_{11}+w_{12}x_{12}+w_{13}x_{13}\\ = w_{21}x_{21}+w_{22}x_{22}+w_{23}x_{23}\\ = w_{31}x_{31}+w_{32}x_{32}+w_{33}x_{33}\\ \end{align*} $$
두 번째 가중 합산
$$ \begin{align*} y_{12}= w_{11}x_{12}+w_{12}x_{13}+w_{13}x_{14}\\ = w_{21}x_{22}+w_{22}x_{23}+w_{23}x_{24}\\ = w_{31}x_{32}+w_{32}x_{33}+w_{33}x_{34}\\ \end{align*} $$
이와 같이 슬라이드 형태로 연산한다.

슬라이딩의 순서는 위와 같다.
Convolution Network에서 연산
Convolution Network는 이미지의 특징을 추출하기 위해 convolution filter를 학습하며, 특징의 추상화 수준에 따라 convolution 연산을 여러 단계로 계층화하여 실행한다.
- 데이터에 내포된 다양한 특징을 추출할 수 있게 특징에 따라 별로의 filter를 두며 데이터의 특징이 다양하다면 여러 개의 filter를 두어야 한다.
- filter의 크기와 개수는 계층별로 특징의 추상화 수준에 따라 다르게 설계한다. 추상화 수준이 놓아질수록 특징이 세분화되므로 더 많은 종류의 필터가 필요하다.
- filter 값은 데이터의 특징을 잘 추출할 수 있도록 학습을 통해 정한다. 즉, 미리 설계된 convolution filter가 아닌 이미지에 따라 최적의 값으로 학습 과정에서 결정한다.
이미지 입력의 형태
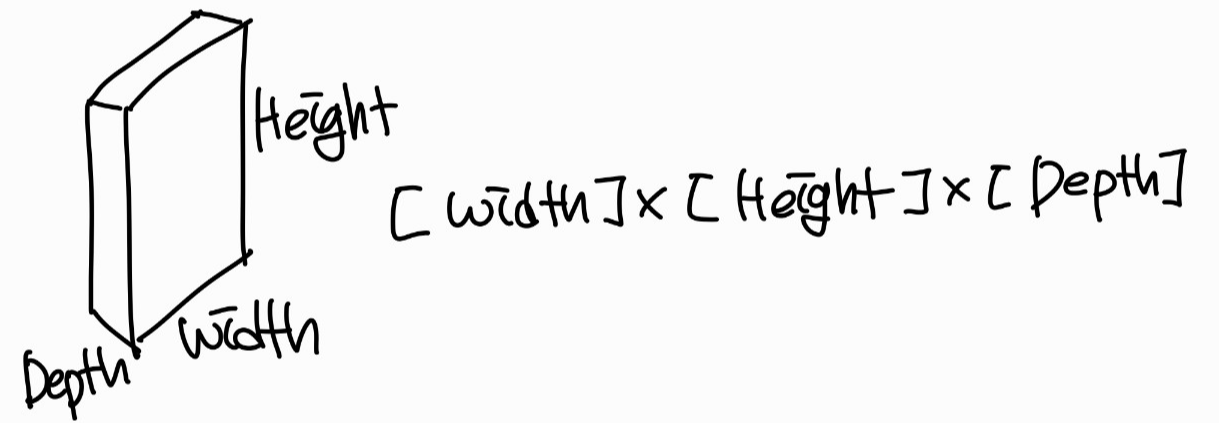
Width x Height는 이미지의 크기이고 Depth는 RGB 색상을 나타낸다.
RGB는 흑백이라면 =1, 컬러라면 =3, 투명도까지 고려한다면 =4로 설정할 수 있다
Filter의 형태
filter를 kenel이라고 부르기도 한다.
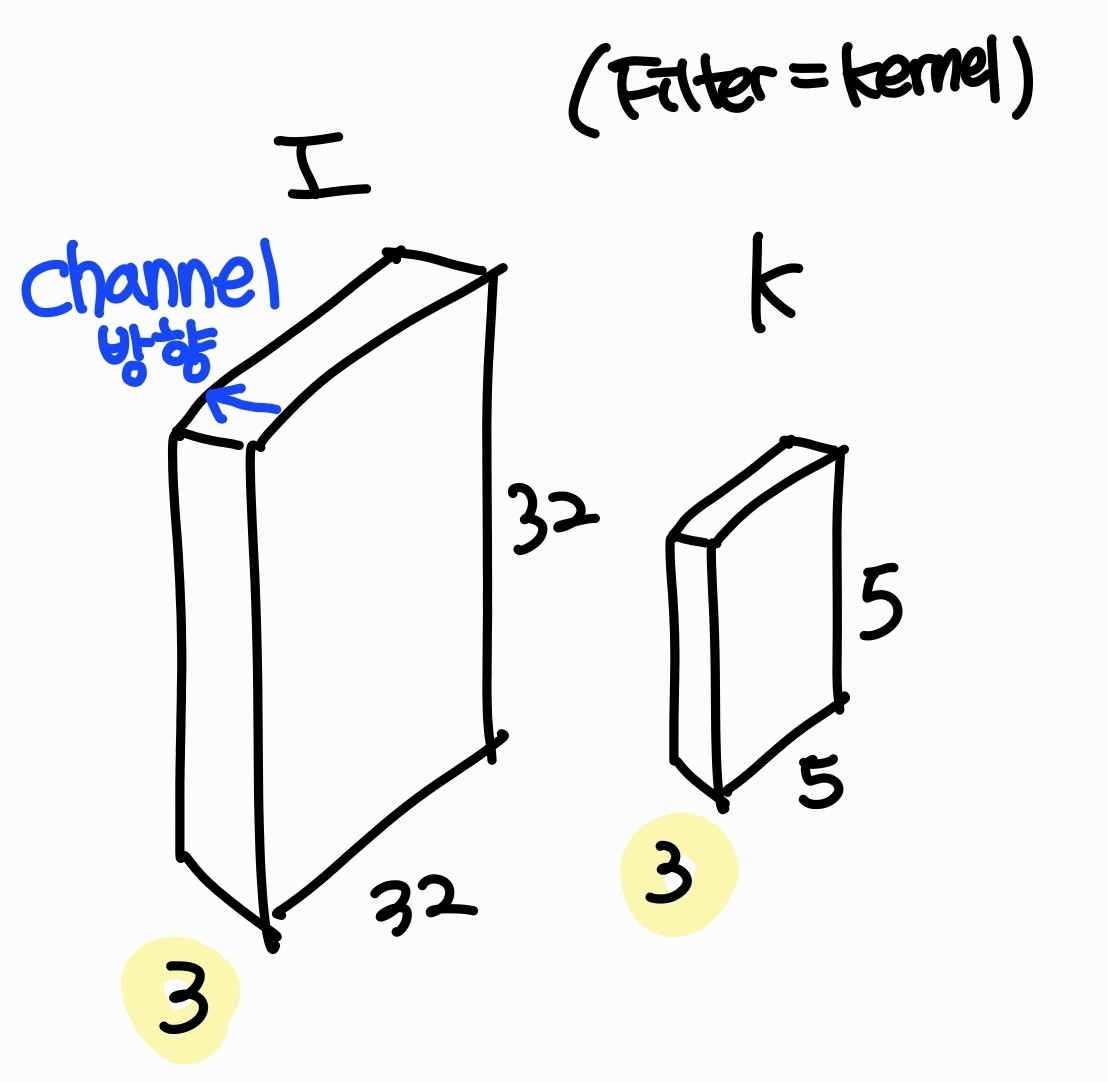
filter도 이미지와 같이 width, height, channel로 3차원으로 이루어져 있으며 channel 방향으로는 슬라이딩을 하지 않기 때문에 image와 filter의 channel 개수는 같아야 한다.
Filter 크기
뉴런의 수용 영역은 filter의 크기에 따라 달라지며 모든 계층에서 작은 filter를 쓴다면 수용 영역을 조금씩 늘려가며 특징을 학습하고 큰 filter를 쓴다면 수용 영역을 빠르게 확장하며 특징을 학습하게 된다.
filter의 크기에 따라 신경망의 성능이 달라지며 filter의 크기는 신경망의 성능이 최대화되도록 정해야 한다. 일반적으로 3x3, 5x5, 7x7을 사용한다.
Filter 개수
이미지의 복잡도에 따라 달라지며 filter마다 다른 특징을 학습하기 때문에 이미지 특성이 다양할수록 많은 filter를 사용해야 한다.
표준 convolution 연산
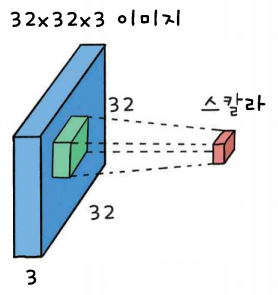
2차원 이미지와 같이 슬라이딩 연산을 하며 모든 channel이 한꺼번에 가중합산을 한다.
뉴런
그렇다면 뉴런은 어디에 존재하는 것일까? filter 하나가 가중 합산 연산을 할 때마다 하나의 뉴런이 실행되는 것과 같다.
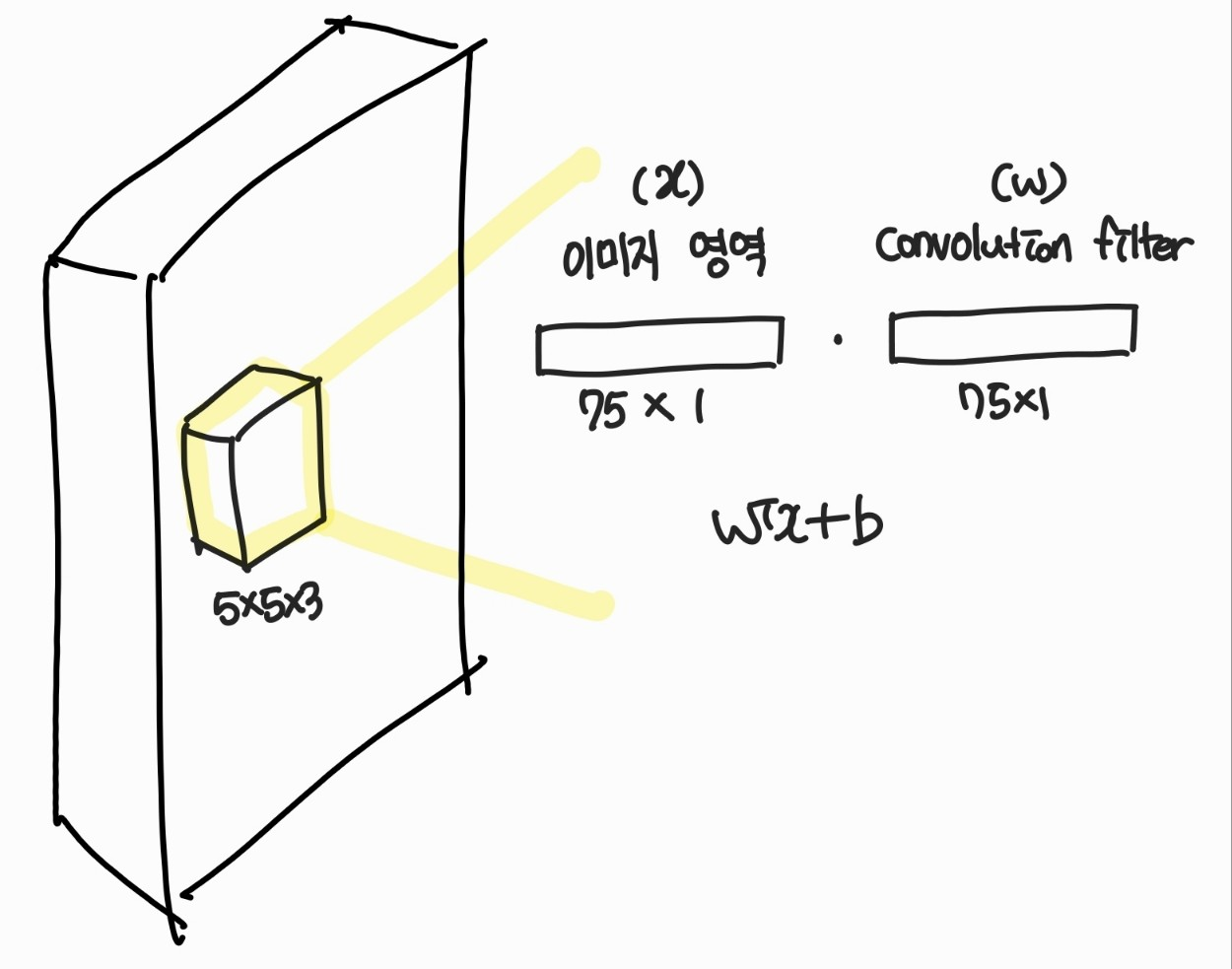
convolution 연산 중 겹쳐진 5x5x3 이미지 영역과 filter를 크기가 75인 1차원으로 변환해 보면 위의 그림과 같고 convolution 연산 벡터의 내적을 표현할 수 있다.
지역 연결

Feedforward Network(full connectivity)와 달리 CNN은 지역 연결(local connectivity)을 갖는 뉴런으로 가중치 filter는 모든 뉴런에서 재사용된다. 따라서 convolution network의 뉴런은 지역 연결을 가지면서 가중치는 공유하는 뉴런이다.
Activation map
convolution 연산 결과로 만들어지는 이미지를 액티베이션 맵이라고 한다. 뉴런의 출력을 액티베이션이라고 한다. 또한 입력 데이터의 특징을 추출한 결과이기 때문에 피처 맵(Feature Map)이라고도 부른다.
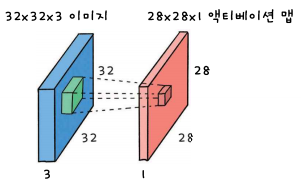
activation map의 픽셀은 각 뉴런의 출력이다. 따라서 한 계층에는 activation map과 같은 3차원 텐서 형태로 뉴런들이 모여 있다고 생각할 수 있다.
activation map은 filter의 크기만큼 지역 연결을 가지며 입력 데이터의 지역 특성을 학습한다. 또한 가중치를 공유하기 때문에 학습된 특징을 위치에 상관없이 인식할 수 있다. 이러한 성질을 이동등변성(transiation equivariance)라고 한다.
filter의 개수가 activation map의 channel 수이며 N개의 filter가 있다면 N개의 channel을 가지는 activation map이 만들어진다.

'Vision' 카테고리의 다른 글
| [CNN] CNN의 성질 (0) | 2023.01.26 |
|---|---|
| [CNN] 서브샘플링 Subsampling (0) | 2023.01.25 |
| [CNN] Convolutions 사용 이유 (0) | 2022.11.28 |
| [CNN] LeNet-5 구조 (0) | 2022.10.13 |
| [CNN] CNN 풀링 Pooling (0) | 2022.10.11 |
