CNN은 뉴런이 지역 연결을 갖는 모델이기 때문에 parameter의 일부만 사용한다. 사용하지 않는 parameter는 해당 parameter의 확률이 없는 것으로 간주하는 매우 강한 사전 분포(Infinitely Strong Prior)를 가정한다. 이런 가정하에 convolution 연산과 pooling 연산이 정의되었기 때문에 CNN은 희소 연결(Sparse connectivity)을 갖고 파라미터 공유를 하는 구조를 가지게 되고 이동 등변성(Translation equivariance)과 위치 불변성(Positional invariance)을 갖는다.
위와 같은 구조와 성질을 가지고 있기 때문에 공간 데이터 처리시에 성능이 극대화 된다.
연산 성질
Convolution 연산은 일부 파라미터를 사용하지 않는 매우 강한 사전 분포를 가정한다. filter와 입력 데이터가 겹친느 영역에만 연결되고 나머지 영역에서는 연결이 없는 희소 연결을 가진다. 또한 동일한 CNN은 희소 연결을 가지고 파라미터 공유를 하므로 위치에 상관없이 동일한 지역 특징을 인식할 수 있다(이동 등변성).

희소 연결 성질
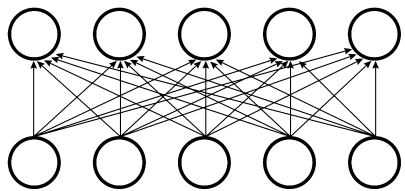
Infinitely Strong Prior이 가정되지 않았다면 full connectivity를 가지게 되고 이렇게 된다면 parameter의 수는 \( O(m\times n ) \)이 된다. (입력 =\( m \), 뉴런 = \( n \) )
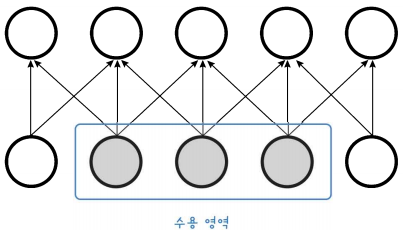
반면 Infinitely Strong Prior를 가정한다면 희소 연결을 가지기 때문에 파라미터 수가 \( O(k\times n) \) 이 된다. (뉴런 = \( n \), 뉴런에 연결된 입력 = \( k \) )
이동등변성
파라미터를 공유하기 때문에 위치에 상관없이 특징을 인식하는 성질이다.
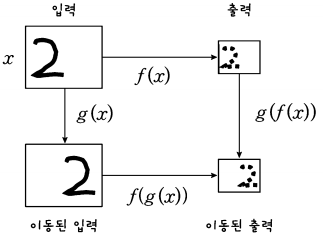
위의 사진의 숫자 2가 이동하였어도 파라미터가 모든 뉴런을 돌기 때문에 위치는 달라졌어도 같은 특징을 인식하는 것을 알 수 있다.
이를 함수 관계로 표현할 수 있다. 이동 변환을 \( g(x) \)라고 하고 convolution 연산은 \( f(x) \)라고 하면 입력 데이터 \( x \)를 이동한 뒤에 convolution한 결과는 \( f(g(x)) \)가 되고, 입력 데이터 x를 convolution한 뒤에 이동한 결과는 \( g(f(x)) \)가 된다. 다음과 같이 이 두 결과가 같으면 이동 등변성을 가진다.
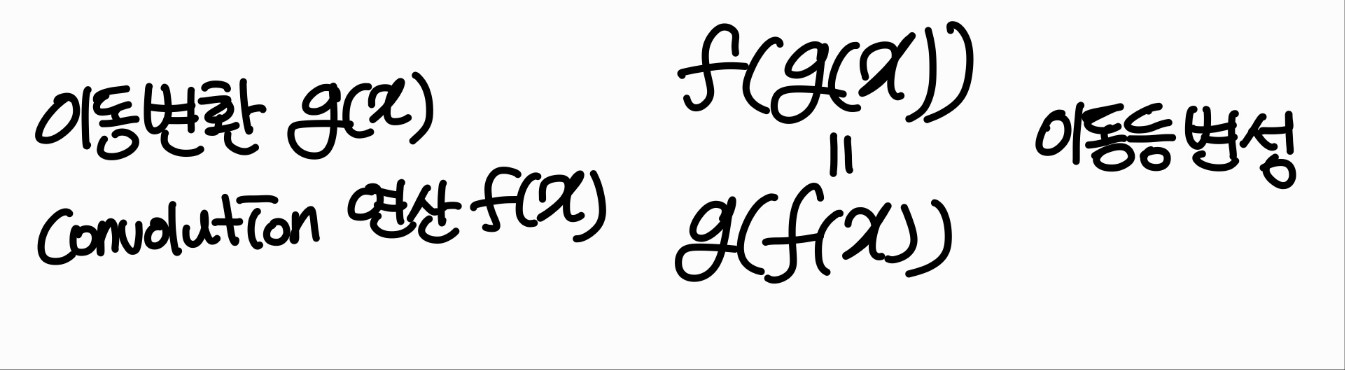
이동 변환에 대해서는 등가 성질을 가지지만 조정, 회전에 대해서는 등가 성질을 가지지 않기 때문에 이와 같은 경우에는 조정, 회전 데이터셋을 추가로 넣어서 학습시키면 된다.
풀링 연산 성질
풀링 연산 또한 수용 영역 외의 파라미터는 쓰지 않는다. 풀링 연산은 위치불변성을 가진다.
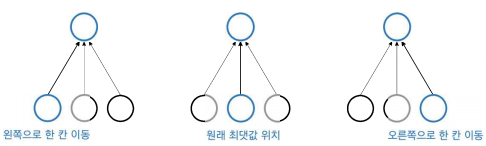
위의 그림을 max pooling 한다고 하였을 때 3가지 경우의 결과는 동일하다. 이처럼 아주 작게 이동했을 때 출력이 바뀌지 않는 성질을 위치불변성이라고 하고 함수적 표현은 아래와 같다.

'Vision' 카테고리의 다른 글
| [CNN] 업샘플링 Upsampling (0) | 2023.01.27 |
|---|---|
| [CNN] 개선된 convolution 연산 (0) | 2023.01.26 |
| [CNN] 서브샘플링 Subsampling (0) | 2023.01.25 |
| [CNN] CNN의 구조 (0) | 2023.01.25 |
| [CNN] Convolutions 사용 이유 (0) | 2022.11.28 |
