규제, 가중치 감소

$$ w^{T}x+b=0 $$
\( w^{T}x+b=0 \)에 2를 곱하면 \( 2w^{T}x+2b=0 \)이 되고 이 두 방정식은 같은 직선을 표현하게 됨
그렇다면 위의 2개의 직선중 어떤 방적식을 사용하는 것이 좋을까?
정답은 가중치와 편향을 작게 만드는 방정식을 사용하는 것이다. 가중치 감소(Weight decay)는 학습 과정에서 작은 크기의 가중치를 찾게 만드는 정규화 기법이다.
가중치 감소 적용 방식
가중치의 크기를 제한하는 제약 조건으로서 손실 함수의 일부 항으로 표현할 수 있음 손실 함수로 확장해서 가중치의 크기를 표현하는 정규화 항(Regularization term)을 더하면, 최적화 과정에서 원래의 손실 함수와 함께 정규화 항도 같이 최소화 되므로 크기가 작은 가중치 해를 구할 수 있음

$$ \widetilde{J}(w)=J(w)+\lambda R(w) $$
\( \lambda \)는 가중치 상수로서 가중치의 크기를 조절하는 역할을 함
\( \lambda \)가 커질수록 정규화 항 비중이 커지면서 가중치 크기는 작아지고 \( \lambda \)가 작을수록 정규화 항 비중이 작아지면서 가중치 크기는 커짐
이를 통해 \( \lambda \)가 모델의 복잡도를 조정하는 역할을 한다고 볼 수 있음
\( R(w) \)은 가중치 크기를 나타내는 노름으로 정의하며 \( L_{2} \) 노름을 사용하면 \( L_{2} \) 정규화라고 하고 \( L_{1} \)노름을 사용하면 \( L_{2} \) 정규화라고 함
각각 리지 회귀 Ridge Regression, 라소 회귀 Lasso Regression이라고 함
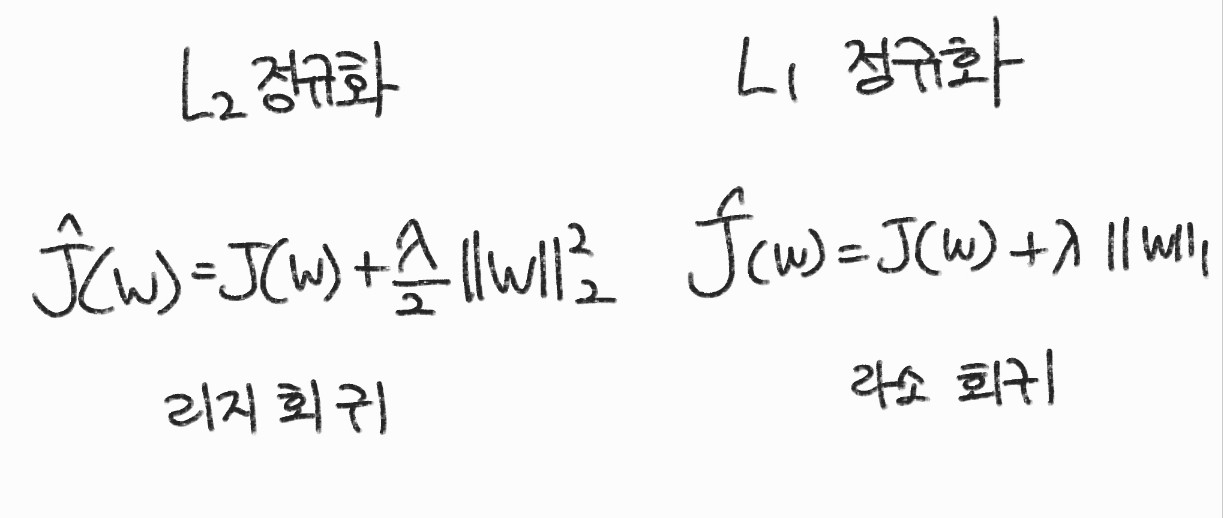
가중치 사전 분포와 노름
가중치의 사전 분포가 가우시안 분포라면 \( L_{2} \) 노름을 사용하고, 라플라스 분포(Laplace distribution)라면 \( L_{1} \) 노름을 사용한다. 가중치의 분포를 모른다면 보통 \( L_{2} \) 노름을 사용함

정규화 효과
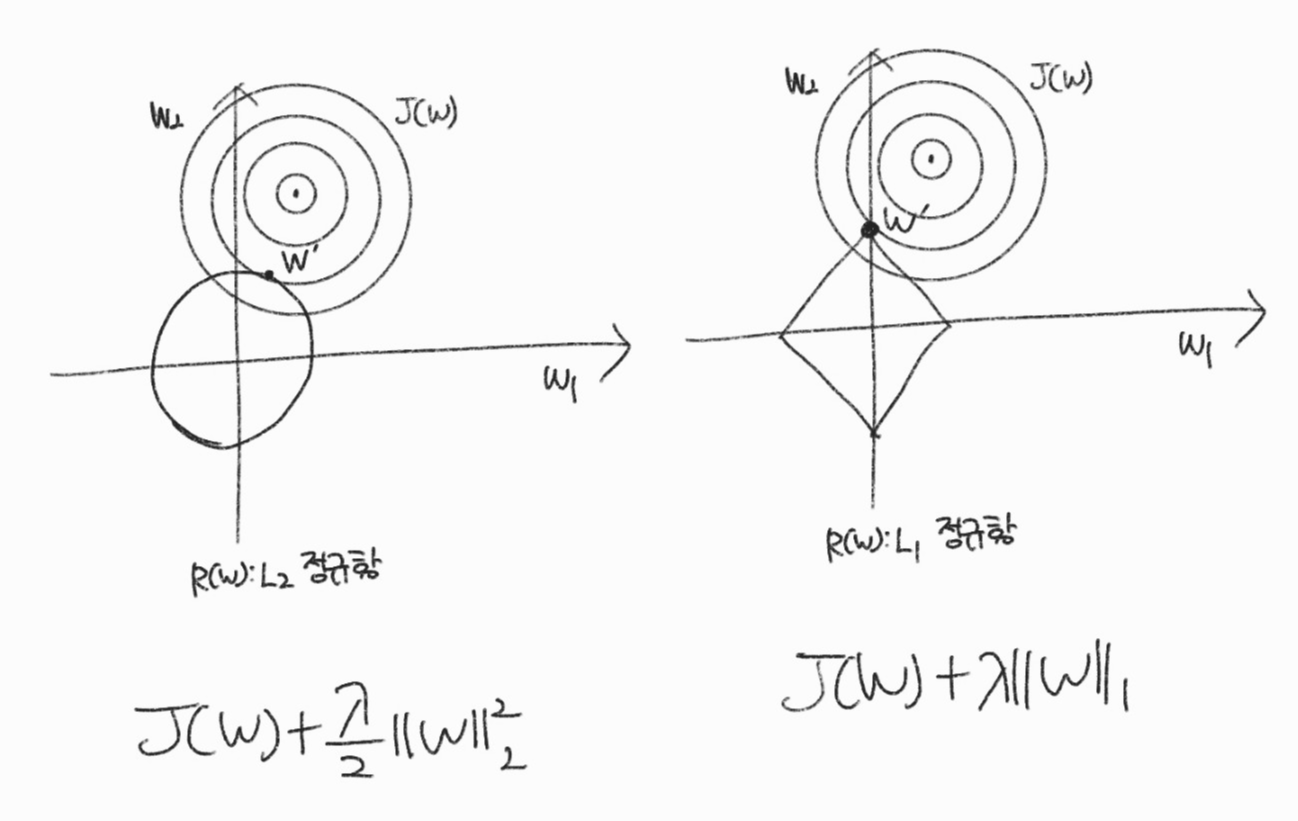
원형 등고선과 동그라미와 다이아몬드가 만나는 접점이 가중치를 감소한 확장된 손실 함수의 해가 된다. L2는 원이기 때문에 최적해는 원점 주변에 위치하며 L2는 다이아몬드 모서리에 먼저 닿을 확률이 높아 가중치가 희소해질 수 있음
가중치가 희소해지면 유효 파라미터가 줄어들어 작은 모델이 된다.
'Machine Learning > 이론' 카테고리의 다른 글
| [ML] 인공지능 기초, 개요 (0) | 2023.04.12 |
|---|---|
| [미분] 미분 기초와 모델 학습에 쓰이는 미분 (1) | 2023.03.20 |
| [ML] 신경망 학습, 학습 최적화 (0) | 2023.01.07 |
| [ML] 신경망 학습시 주의사항 (0) | 2023.01.06 |
| [ML] 신경망 모델의 크기 (0) | 2023.01.06 |
