미분(Derivatives)
도함수라고도 하며 x가 변화할 때 y의 변화량으로 한 점의 기울기로 볼 수 있음
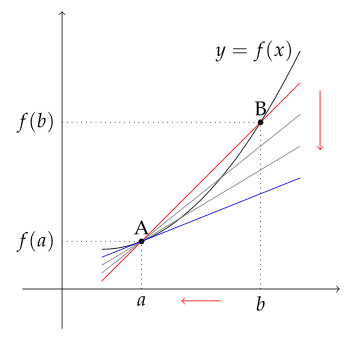
평균 변화율
$$ \frac{f(b)-f(a)}{b-a} $$
x가 변할 때 y의 변화량
순간변화율
$$ f'(x) = lim_{h \rightarrow 0} \frac{f(x+h)-f(x)}{h} $$
평균 변화률의 극한값으로 한 점의 기울기
a의 접선의 기울기
직선 미분
\( f(x) = 3x \) 이라는 함수가 있을 때,
\( x = 2 \), \( f(x) = 6 \)
\( x = 2.001 \), \( f(x) = 6.003 \)
3만큼 변화한다고 할 수 있고 derivative = 3이 된다.
$$ \frac{ \partial f(x)}{ \partial x} = \frac{ \partial }{ \partial x} =3 $$
곡선 미분
손실함수는 convex한 모양을 가지기 때문에 곡선에서의 미분을 이해해야 한다.
\( f(x) = x^{2} \) 이라는 함수가 있을 때,
\( x = 2 \), \( f(x) = 4 \)
\( x = 2.001 \), \( f(x) = 4.004 \)
\( \frac{ \partial f(x)}{ \partial x} = 4, when \ x=2 \)
\( x = 5 \), \( f(x) = 25 \)
\( x = 5.001 \), \( f(x) = 25.010 \)
\( \frac{ \partial f(x)}{ \partial x} = 10, when \ x=5 \)
$$ \frac{ \partial f(x)}{ \partial x} = \frac{ \partial }{ \partial x}x^{2} =2x $$
Chain rule
Neural Network는 순전파와 역전파를 통해 Gradient를 계산하는데 이는 모델이 여러 layer를 가지고 반복적으로 학습하기 때문이다.
$$ J(a,b,c) = 3(a+bc) $$
$$ u = bc $$
$$ v = a+u $$
$$ J = 3v $$

\( \frac{ \partial J}{ \partial v} \)구하기
위의 식이 있을 때 \( \frac{ \partial J}{ \partial v} \)는 \( v=11 \longrightarrow 11.001, \ j=33 \longrightarrow 33.003 \)이기 때문에 3이 나온다
\( \frac{ \partial J}{ \partial a} \)구하기
$$ \frac{ \partial J}{ \partial a} = \frac{ \partial J}{ \partial v} \times \frac{\partial v}{\partial a} $$
\( \frac{ \partial J}{ \partial a} \)는 \( a=5 \longrightarrow 5.001, \ v=11 \longrightarrow 11.001, \ J=33 \longrightarrow 33.003 \) 통해 \( a \)가 \( v \)를 1만큼 변화시키고 \( v \)가 \( J \)를 3만큼 변화시키기 때문에 3이 나오는 것을 알 수 있다.
미분 공식
기본 공식

몫의 미분
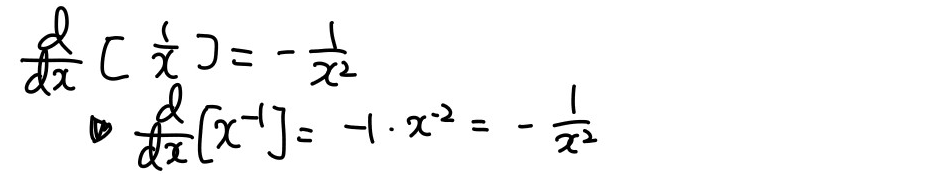
곱의 미분

합성미분
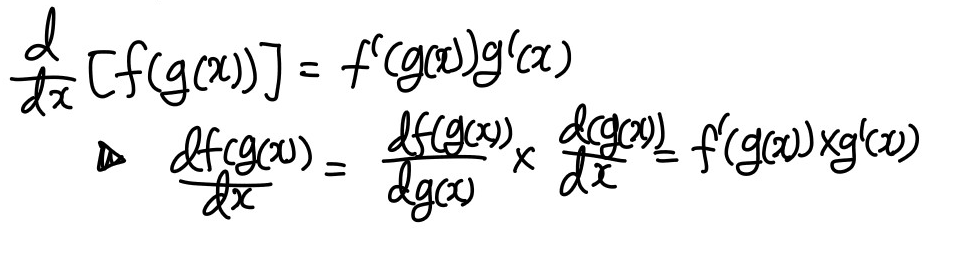
지수함수 미분
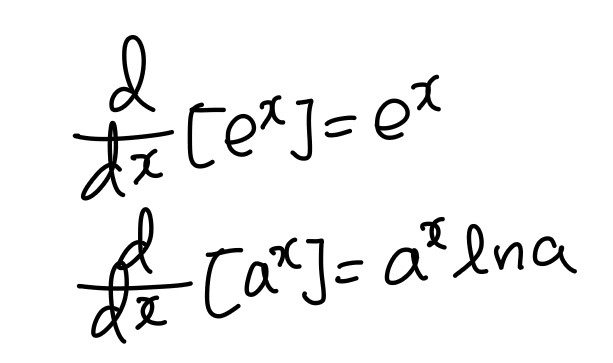
로그함수 미분
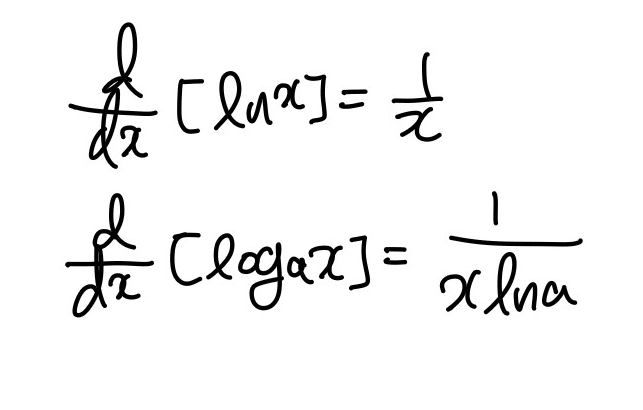
미분 사용 이유
미분을 이용하여 접선의 기울기 함수를 통해 극대값과 극소값을 알아낼 수 있음
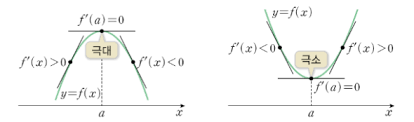
이를 통해 loss function이 낮아지는 구간의 parameter 값을 구할 수 있음
'Machine Learning > 이론' 카테고리의 다른 글
| [통계] 엔트로피 Entropy, 크로스 엔트로피 Cross Entropy, KL divergence (0) | 2023.06.14 |
|---|---|
| [ML] 인공지능 기초, 개요 (0) | 2023.04.12 |
| [ML] 규제, 가중치 감소 (0) | 2023.01.17 |
| [ML] 신경망 학습, 학습 최적화 (0) | 2023.01.07 |
| [ML] 신경망 학습시 주의사항 (0) | 2023.01.06 |
