시그모이드 함수와 크로스 엔트로피 손실
Sigmoid 함수는 분모에 지수항이 있기 때문에 함수의 양 끝부분에서 그레이디언트 포화 문제가 발생한다.
여기서 이를 보완할 수 있는 방법이 있는데 그것은 크로스 엔트로피 손실을 사용하는 방법이다.
출력 계층에서 Sigmoid 함수를 사용할 때 크로스 엔트로피 손실을 사용하면 일부 구간에서 그레이디언트 포화가 생기지 않게 만들 수 있다.
Cross Entropy loss Function
$$ J(\theta) = -\sum_{i=1}^{N}t_{i}\cdot log\mu (x_{i};\theta)+(1-t_{i})\cdot log(1-\mu(x_{i};\theta)) $$
여기서 t = 1 이라고 한다면 \( J(\theta)=-log(\mu(x;\theta)) \)로 정의된다.
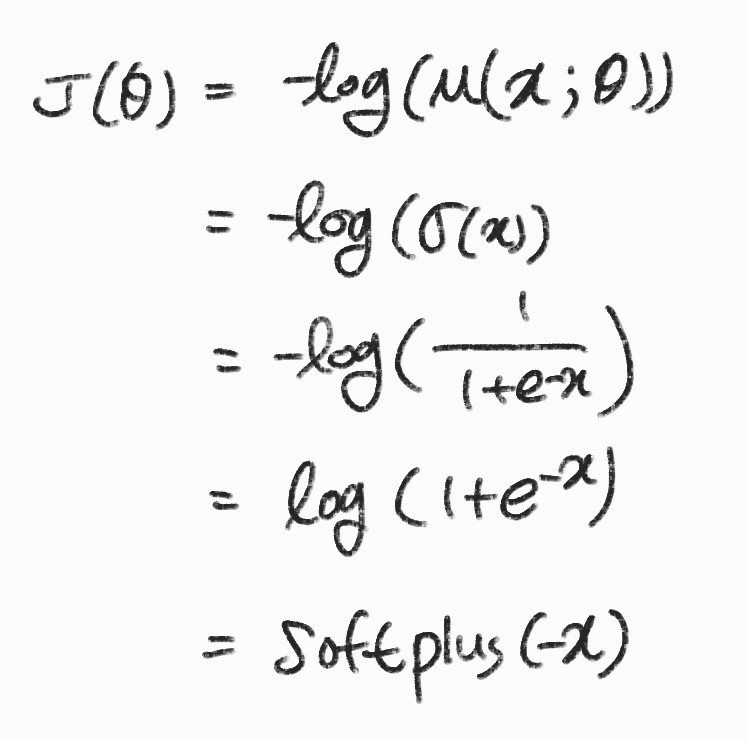
모델의 출력인 \( \mu(x;\theta) \) 부분을 \( \sigma(x) \)로 대체했다.
마지막 줄인 softplus는 부드러운 곡선 형태의 ReLU함수와 유사하다.
Softplus Function
$$ Softplus(x)=\frac{1}{\beta}log(1+e^{\beta\ast x}) $$
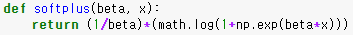
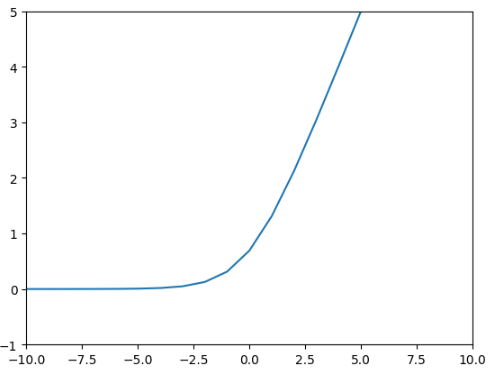
Sigmoid의 지수항이 Cross Entropy loss의 로그 함수에 상쇄되어 Softplus 함수 형태로 변환되었고 그렇기 때문에 양수 구간에서 그레이디언트 포화가 발생하지 않는다.
이와 같이 Sigmoid와 Cross Entropy loss 를 같이 사용한다면 그레이디언트 포화를 예방할 수 있다.
활성화 함수 양수 출력 문제
시그모이드와 ReLU와 같이 활성 함수의 출력이 항상 양수이면 학습 경로의 이동 방향이 크게 진동하면서 학습이 느려진다. 왜 이런 현상이 발생하는 것일까?
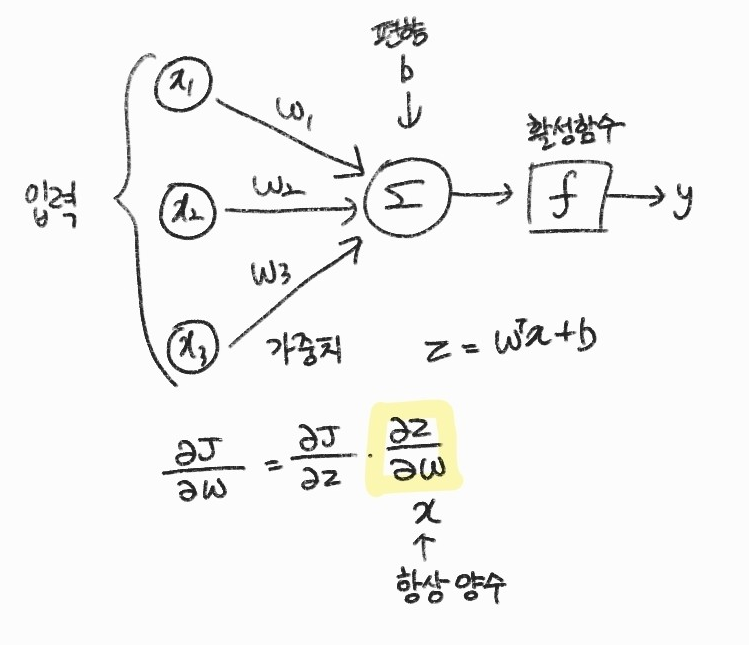
가중치의 그레이디언트
$$ \frac{\partial J}{\partial w} = \frac{\partial J}{\partial z} \cdot \frac{\partial z}{\partial w} $$
여기서 \( \frac{\partial z}{\partial w} \)는 \( z=w^{t}x+b \)를 \( w \)로 미분한 지역 미분 값이기 때문에 항상 \( x \)가 나온다.
따라서 입력 \( x \)가 양수라면 지역 미분 값도 항상 양수가 된다.
\( \frac{\partial J}{\partial z}가 양수라면 그레이디언트 \frac{\partial J}{\partial w} = (\frac{\partial J}{\partial w_{1}},\frac{\partial J}{\partial w_{2}},\cdot, \frac{\partial J}{\partial w_{n}}) \) 모든 차원이 양수가 되고 \( \frac{\partial J}{\partial z} \)가 음수라면 모든 차원이 음수가 된다.
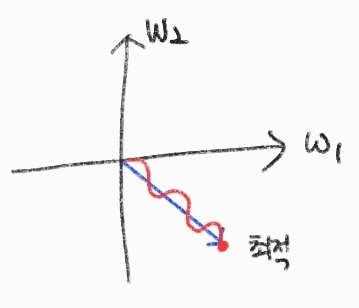
가중치가 2개가 있다고 가정한다면 모든 차원이 음수나 양수로 움직이기 때문에 가중치는 0도에서 90도, 180도에서 270도 방향으로 움직일 것이다.
그렇기 때문에 사진처럼 최적의 해로 가기 위해서는 직선으로 가지 못하고 진동하기에 느리게 도달한다. 따라서 뉴런의 입력값이 항상 양수이면 학습 경로가 진동하면서 학습이 느려진다.
죽은 ReLU가 발생하는 이유
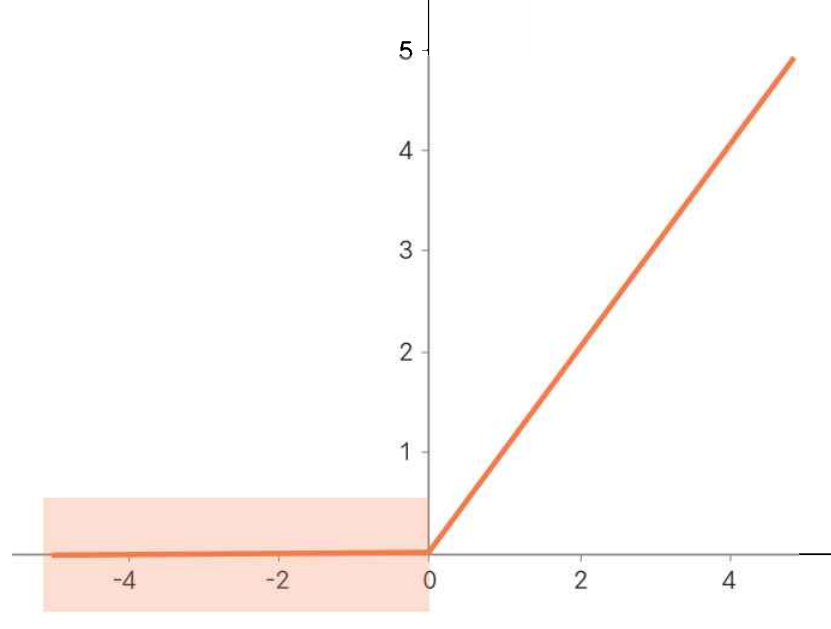
죽은 ReLU는 뉴런이 계속 0을 출력하는 형태를 말하고 이는 가중치 초기화를 잘 못했거나 학습률이 매우 클 때 발생한다.
가중치 초기화를 못했을 때
가중치의 그레이디언트
$$ \frac{\partial J}{\partial w} = \frac{\partial J}{\partial z} \cdot \frac{\partial z}{\partial w} $$
위와 같이 \( \frac{\partial z}{\partial w} \)는 \( x \)이다.
따라서 뉴런의 입력 \( x \)가 크다면 \( \frac{\partial J}{\partial w} \)도 커지게 되고 \( w += w-\alpha \frac{\partial J}{\partial w} \)로 가중치를 업데이트하면 가중치가 큰 음수로 변한다.
가중치가 한 번 음수로 변하면 다음 입력이 들어왔을 때 가중 합산이 음수가 되고 ReLU는 0을 출력하게 된다.
ReLU의 그레이디언트가 0이 되어 학습이 진행되지 않고 계속 0이 된다.
미분 불가능한 활성 함수
신경망에서는 미분 가능한 활성 함수를 사용해야한다고 알고 있는 것이다. 하지만 ReLU와 같은 구간 선형 함수는 구간이 바뀌는 지점에서는 미분이 되지 않는다.
미분이 되지 않는 함수를 사용해도 될까? 답은 사용해도 괜찮다 이다.
신경망은 근사 방식으로 함수를 표현하기 때문에 약간의 미분 오차를 허용해도 결과에 미치는 영향은 크지 않다.
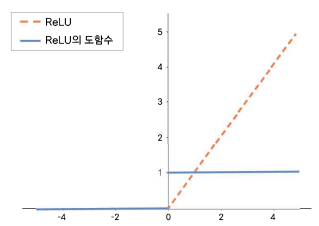
여기서 \( x=0 \)일 때 우미분 1, 좌미분 0중 어느 것을 사용해도 상관이 없다.
'Machine Learning > 이론' 카테고리의 다른 글
| [ML] 규제, 가중치 감소 (0) | 2023.01.17 |
|---|---|
| [ML] 신경망 학습, 학습 최적화 (0) | 2023.01.07 |
| [ML] 신경망 모델의 크기 (0) | 2023.01.06 |
| [ML] 분류와 회귀 문제 (0) | 2023.01.03 |
| [ML] Image data (0) | 2022.09.29 |
