다층 퍼셉트론 = 순방향 신경망 (Feedforward Neural Network)
퍼셉트론 = 인공 뉴런 (Artificial neuron)
CNN (Convolution neural network)는 공간 데이터(image), RNN(Recurrent Neural Network)는 순차 데이터(시계열 데이터)에 주로 사용됨
순방향 신경망의 구조
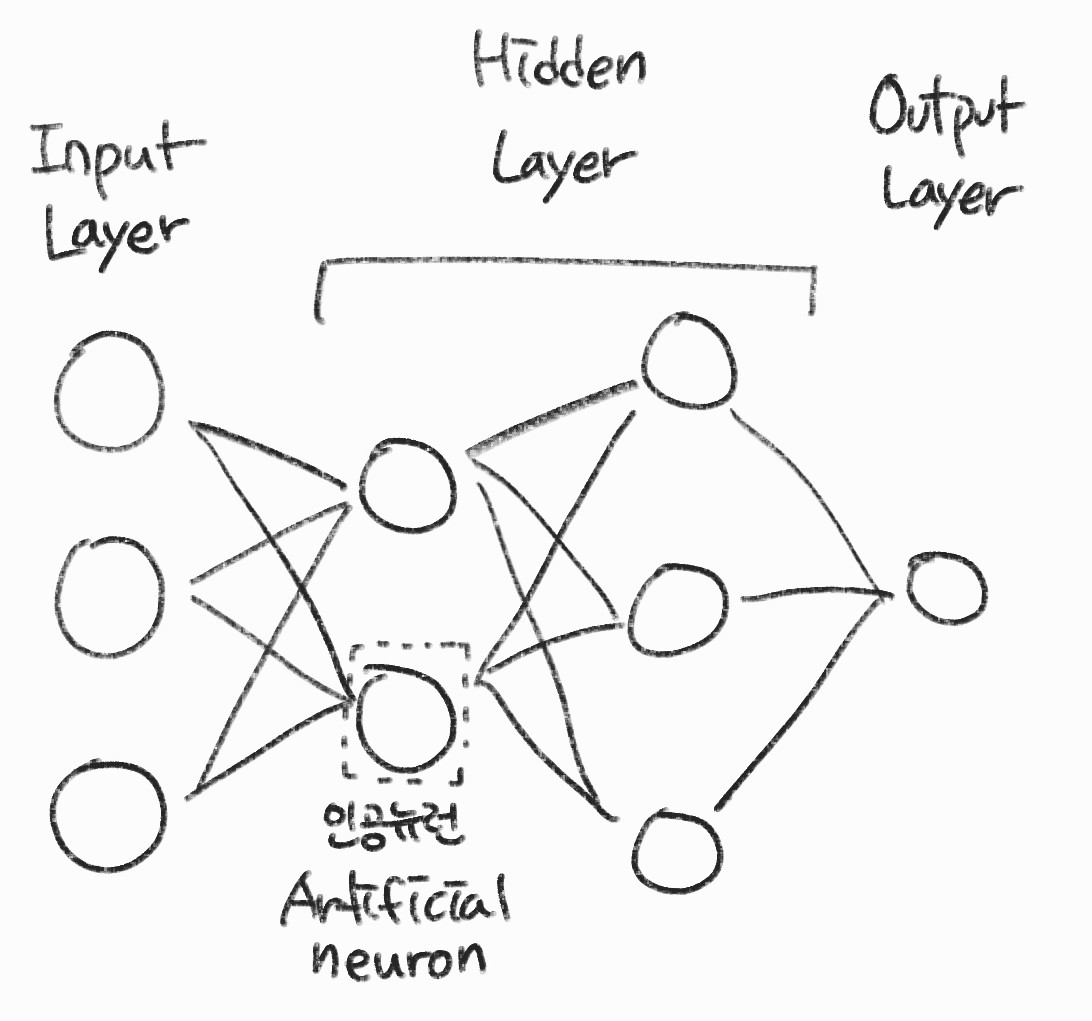
- 입력 계층
- 외부에서 데이터를 받아 전달하는 계층
- 은닉 계층
- 데이터의 특징을 추출하는 계층
- 출력 계층
- 추출된 특징을 기반으로 결과를 외부에 출력하는 계층
- 대부분의 모델에는 입력 계층과 출력 계층이 하나씩 있고 은닉계층만 가변적으로 구성된다.
- 모든 계층이 Fully connected layer로 구성됨
특징 추출
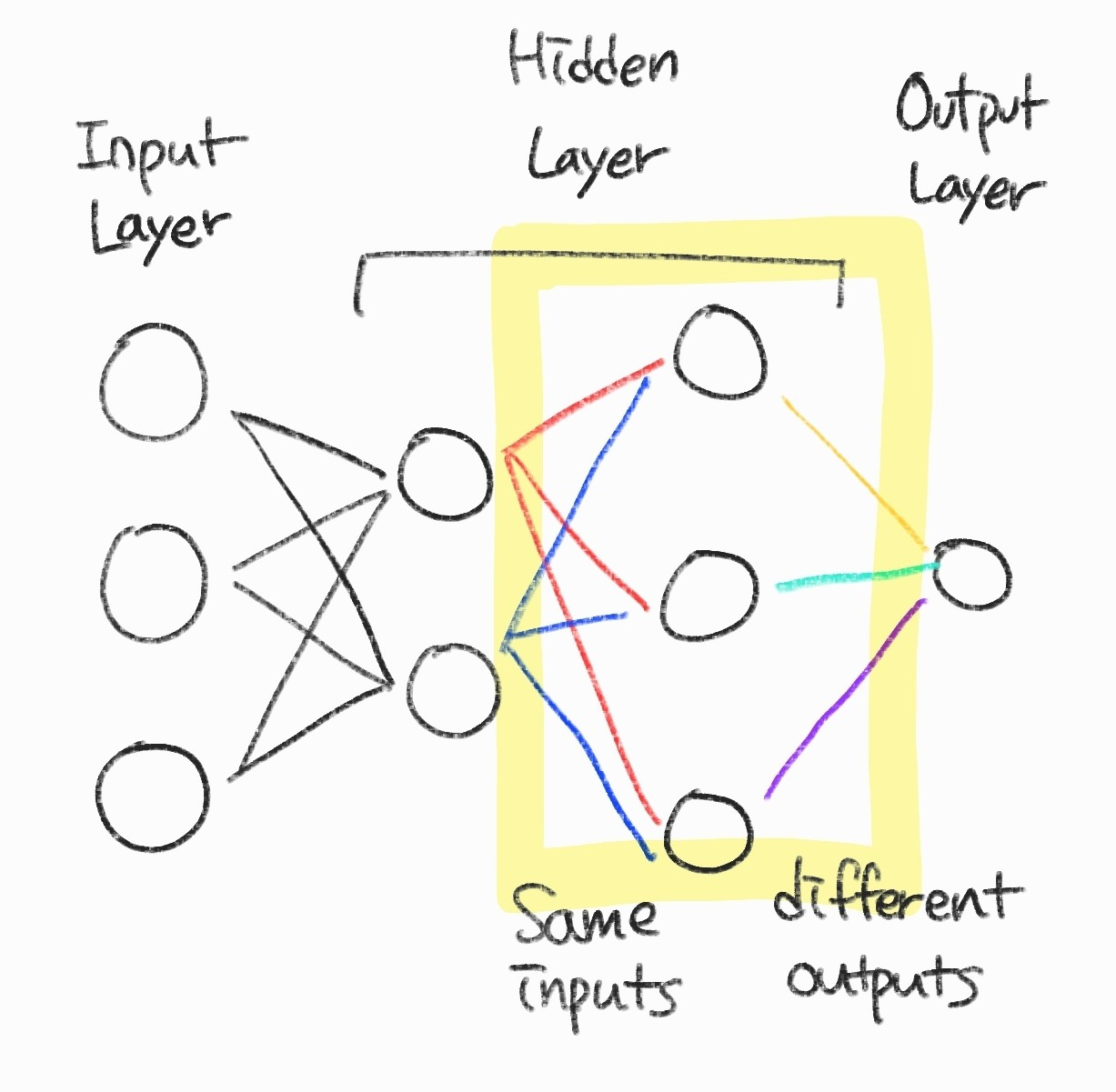
- 각 뉴런은 이전 계층에서 같은 입력을 받고 서로 다른 특징을 추출한다.
- 그렇기 때문에 데이터의 특징이 많다고 판단되면 뉴런의 수를 늘려야지 내재된 특징을 모두 추출할 수 있다.
- 데이터의 이동은 계층 단위로 출력되며 일괄처리한 후 다음 계층으로 보낸다.
- 즉, 신경망에 입력된 데이터는 은닉 계층을 거치면서 추론에 필요한 특징으로 변환되며, 출력 계층은 가장 추상화된 특징을 이용하여 예측한다.
특징 추출 뉴런 구조
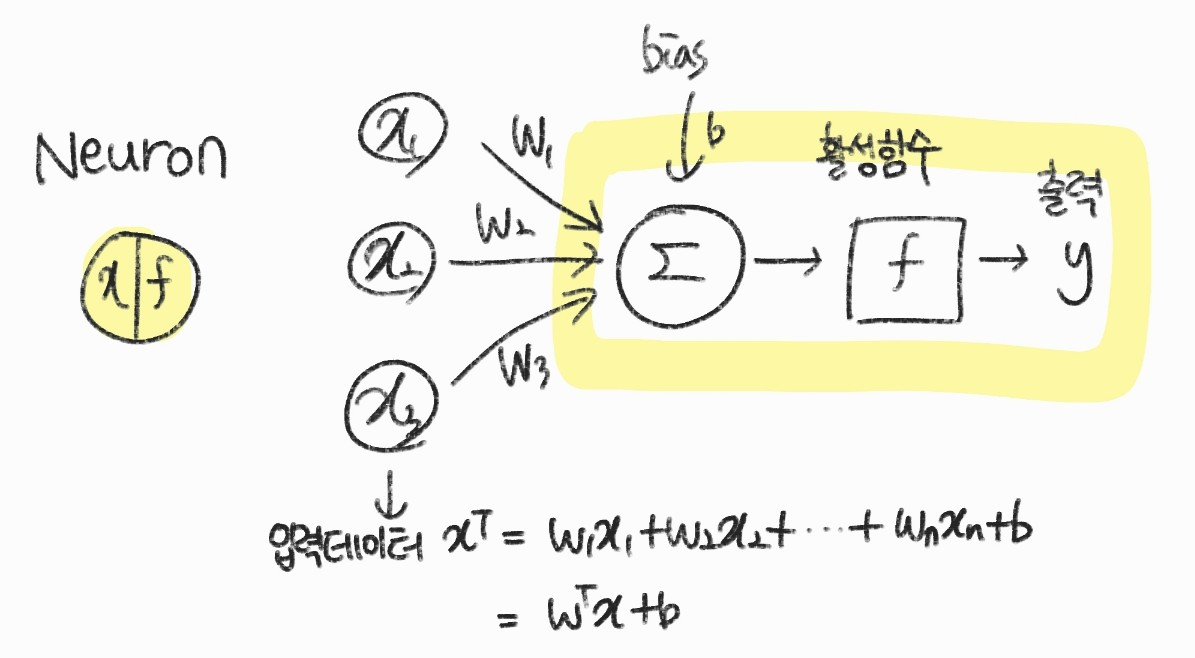
- 뉴런을 확대해서 보면 위와 같은 그림을 그릴 수 있다.
- 출력 y는 다음 계층의 입력으로 들어간다
입력 데이터 : \( x^{T} = (x_{1}, x_{2}, \cdots , x_{n}) \)
가중치 : \( w^{T} = (w_{1}, w_{2}, \cdots , w_{n}) \)
입력 데이터와 가중치를 곱해서 가중 합산을 한다.
$$ z = w_{1}x_{1},w_{2}x_{2},\cdots , w_{n} x_{n}+b = w^{T} x + b $$
가중치는 특징을 추출할 때 영향이 큰 데이터를 선택하는 역할을 함
편향은 편향이 없다면 원점을 지나는 연속 함수이기 때문에 공간상 임의의 위치에 표현하기 위해 사용
활성 함수
https://pasongsong.tistory.com/154
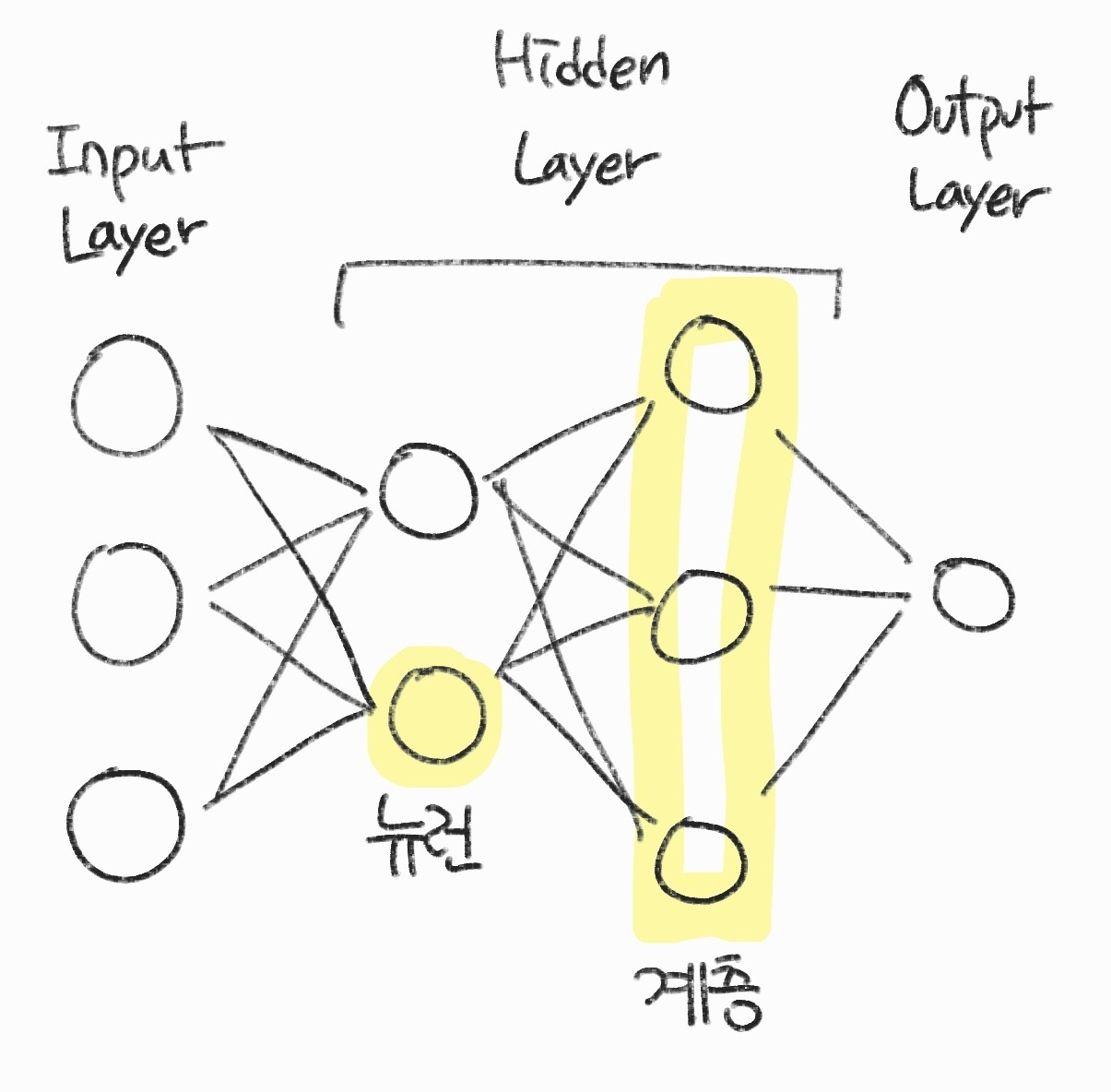
- 신경망은 보통 입력 계층을 제외하고 표기함
- 입력 계층 1개, 은닉 계층 2개, 출력 계층 1개라면 '4계층 신경망'이라고 부름
- 계층이 많아질수록 신경망이 깊어진다고 표현함
- 보통 2 ~ 3 계층일 때 얕은 신경망(shallow neural network) 그 이상을 깊은 신경망(Deep neural network)이라고 한다
실함수 Real-valued function
\( f : \mathbb{R}^{n} \rightarrow \mathbb {R} \) 형태의 함수로 입력은 크기가 n인 벡터이고 출력은 아래와 같이 나온다
$$ f(x) = f(x_{1},x_{2},\cdots,x_{n}) $$
$$ x^{T} = (x_{1},x_{2}, \ldots , x_{n}) $$
벡터함수 Vector function
\( f : \mathbb{R}^{n} \rightarrow \mathbb {R}^{m} \) 형태의 함수로 입력은 크기가 n인 벡터이고 출력은 크기가 m인 벡터로 나온다
$$ f(x) = (f_{1}(x),f_{2}(x), \ldots , f_{m}(x)) $$
$$ x^{T} = (x_{1},x_{2}, \ldots , x_{n}) $$
실함수 뉴런
$$ f(x) = activation(w^{t}x+b) $$
뉴런은 실함수이다.
입력과 가중치를 합산한 결과를 활성 함수에 매핑시켜 실수로 출력하는 합성 함수이다.
입력 : \( x^{T} = (x_{1},x_{2}, \ldots , x_{n}) \)
출력 : \( w^{T} = (w_{1},w_{2}, \ldots , w_{n}) \)
벡터 함수 계층
계층은 벡터 함수이다. 입력도 벡터, 출력도 벡터이다.
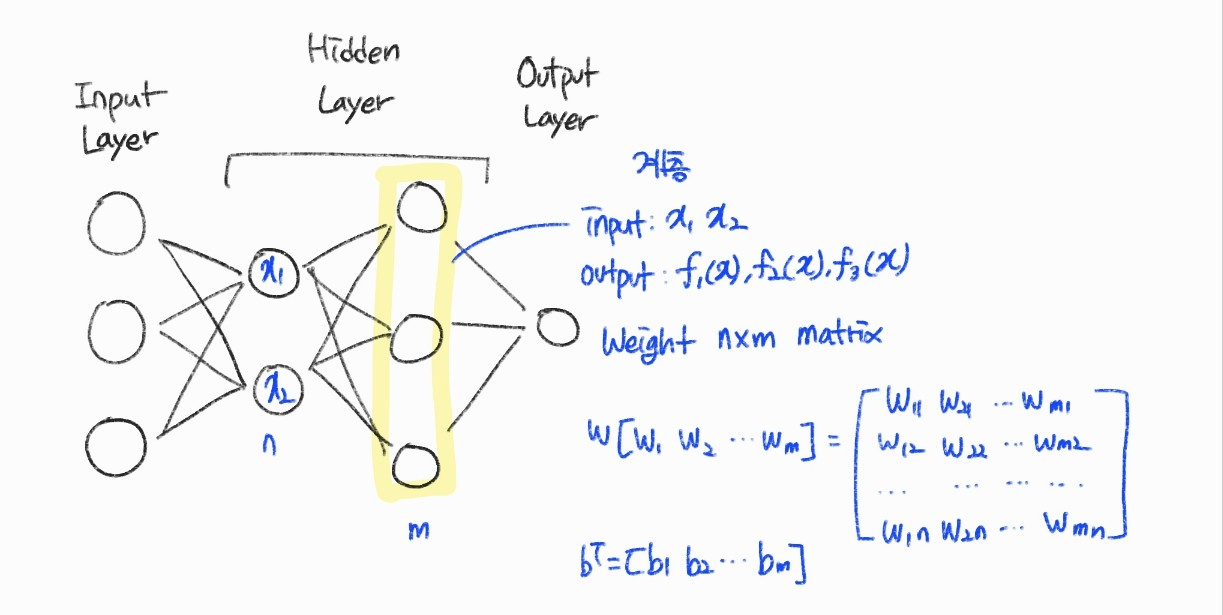
이전 계층의 뉴런 수 : n
현재 계층의 뉴런 수 : m
계층 가중 합산은 가중치 행렬과의 곱 형태로 \( W^{T}x + b \)와 같이 정의가 되며 \( f(x) = activation(W^{t} x+b) \)로 m인 벡터가 출력된다.
신경망 : 벡터 함수들의 합성 함수
신경망의 수가 L이라면 아래와 같은 합성 함수로 정의할 수 있다.
$$ y = f^{L}( \ldots f^{2}(f^{1}(x))) $$
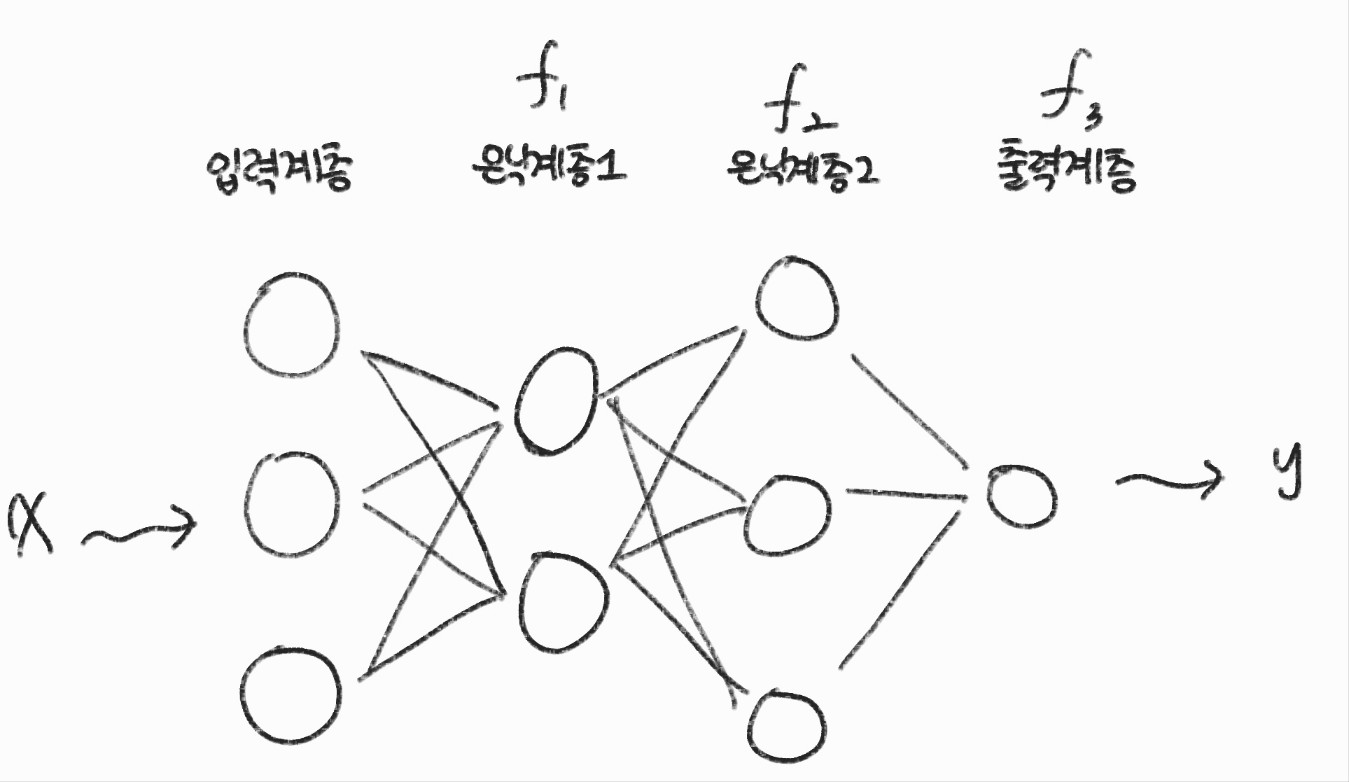
$$ y = f^{3}(f^{2}(f^{1}(x))) $$
신경망의 입력 x를 출력 y로 매핑하는 \( y = f(x; \theta ) \) 형태의 파라미터 함수이며 \( \theta \) 는 뉴런의 가중치와 bias를 포함한 함수의 파라미터이다.
신경망을 학습할 때 미분을 사용하기 때문에 신경망이 표현하는 함수는 미분 가능한 함수(differentiable function)이어야 한다.
범용 근사 정리
신경망은 n 차원 공간의 임의의 연속 함수를 근사하는 능력이 있으며 임의의 연속 함수를 근사할 수 있다는 것은 입출력 관계가 함수로 표현되는 회귀 문제에서 매우 복잡한 예측 곡선을 만들 수 있다는 것을 의미한다.
-> 2계층의 순방향 신경망에서 은닉 뉴런을 충분히 사용하고 검증된 활성 함수를 사용하면 n차원 공간의 임의의 연속 함수를 원하는 정도의 정확도로 근사할 수 있다
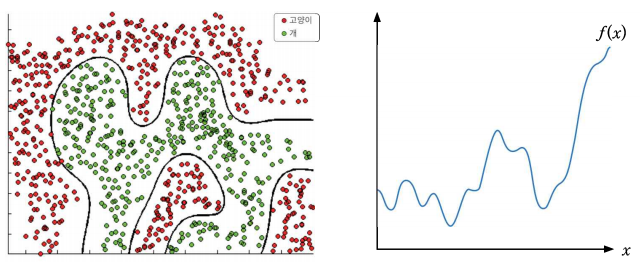
신경망이 범용 근사기(Universal Approximator)라는 것을 범용 근사 정리(Universal Approximation Theorem)로 증명되었다.
범용 근사 정리에 따르면 아주 복잡한 함수를 정확히 근사하기 위해서는 은닉 뉴런을 충분히 사용하여야 한다. 하지만 이 경우에는 과적합이 발생하고 성능이 낮아질 수 있다.
이러한 점을 보완하기 위해 deep Neural Network가 발명되었고 범용 근사 정리가 갖는 문제를 해결할 수 있었다.
이렇게 계층을 쌓아서 만드는 모델은 신경망의 합성 함수 복잡도에 따라 뉴런과 계층을 늘리고 줄임으로써 모델을 쉽게 확장할 수 있고 머신러닝 모델과 비교했을 때 매우 강력하다.
순방향 신경망 설계
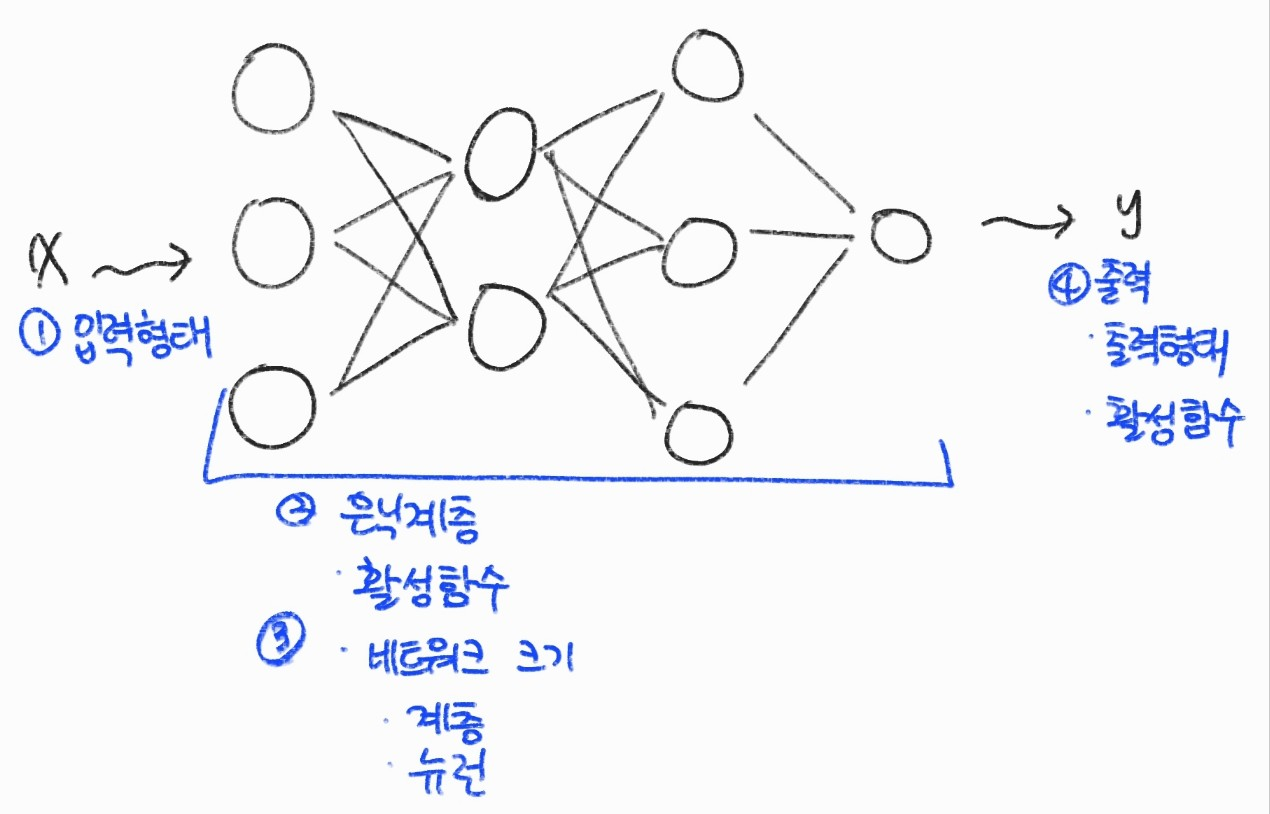
FNN 모델 설계를 위해서 정해야 하는 항목은
- 모델의 입력과 출력 형태
- 활성 함수릐 종류
- 네트워크 크기
등을 고려해야한다.
일반적으로 문제 정의와 신경망 모델의 종류가 선정되면 입력 출력의 형태는 어느 정도 결정이 되고 모델의 크기와 신경망 모델의 종류는 탐색해야 하는 항목이다.
'Machine Learning > Model' 카테고리의 다른 글
| [ML] 나이브 베이즈(Naive bayes) 개념, 실습 (0) | 2023.03.21 |
|---|---|
| [ML] 이진 분류 모델 (0) | 2023.01.03 |
| [DATA] Custom Image Data 넣기 (0) | 2022.12.28 |
| [CNN] CNN Stride (Convolution Neural Network) (0) | 2022.09.29 |
| [CNN] CNN 패딩 Padding (Convolution Neural Network) (2) | 2022.09.29 |
