활성함수 Activation Function

- 신경망에 비선형성을 추가하기 위해 사용함
- 종류
- 이진 활성화 함수 binary step function
- 선형 활성화 함수 linear activation function
- 비선형 활성화 함수 non-linear activation fucntion
- 대부분 비선형 함수를 사용함 (선형 함수를 사용할 경우 역전파가 불가능(도함수가 상수이기 때문) 하고 몇 개를 쌓아도 선형 함수이기 때문에 모든 모델은 선형 회귀 모델로 작동함)
S자형 곡선 함수
Binary Step Function
S형과 유사하지만 곡선 함수는 아님
- \( 0 for X<0 \)
- \( 1 for X>=0 \)


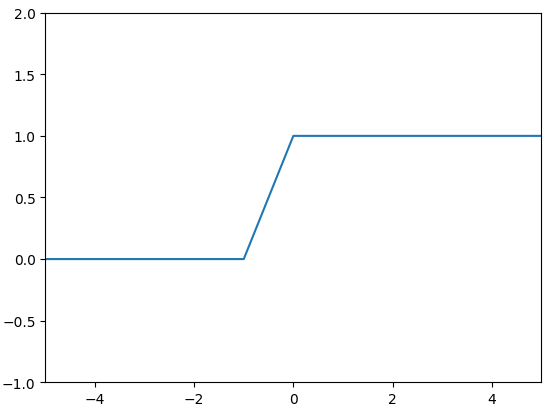
x값을 정수형으로 주어서 그림 2와 같은 그래프가 나왔지만 그림 1과 같은 그래프 형태가 맞음
단점
- multi-class classification 문제에 쓸 수 없음
- 기울기가 0이기 떄문에 오차역전파를 쓸 수 없음
Sigmoid Function
계단 함수와 같이 [0, 1] 범위를 가지고 있다.
모든 구간에서 미분이 가능하고 증가함수이기 때문에 미분값은 항상 양수로 나온다.
$$ \sigma (x) = \frac{1}{1+e^{-x}} $$


Differential Sigmoid function
$$ \frac{d}{dx} sigmoid(x) = sigmoid(x)(1-simoid(x)) $$

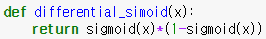
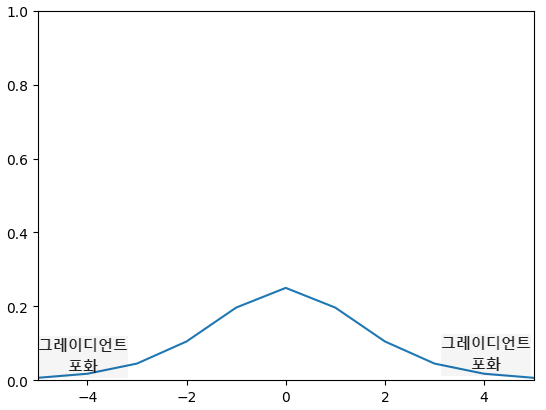
단점
- 지수 함수가 포함되어 있어 연산 비용이 많이 든다.
- 그레디언트 포화가 발생하여 학습이 중단될 수 있다.
- 양수만 출력하기 때문에 학습 경로가 진동하면서 학습 속도가 느려진다.
그레디언트 포화(Gradient saturation)
시그모이드 함수 양 끝 값의 미분값이 0으로 포화되는 상태를 말한다.
함수에서 포화란 입력값이 변화해도 함숫값이 변화하지 않는 상태를 말한다.
이는 기울기 소실(gradient vanishing)로 이어지며 학습이 진행되지 않게 된다.
Tanh(hyperbolic tangent) Function
[-1, 1]의 범위를 가지고 있고 sigmoid 함수의 양수 출력 문제를 해결하고자 고안된 함수이다.
$$ tanh(x) = \frac{e^{x}-e^{-x}}{e^{x}+e^{-x}} $$
Sigmoid의 선형 변환식으로 나타낼 수 있음
$$ tanh(x) = 2\sigma(2x)-1 $$

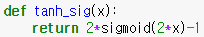
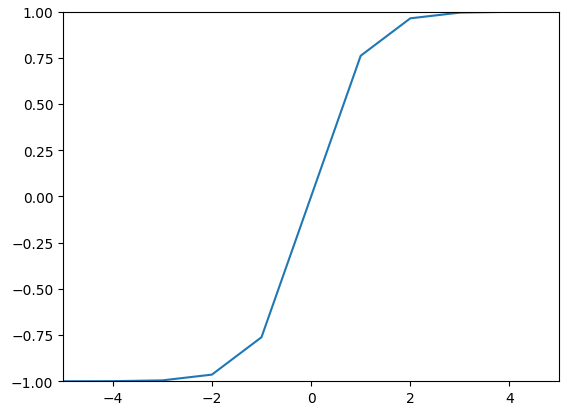
Differential Sigmoid Function
$$ \frac{d}{dx} tanh(x) = 1 - tanh(x)^{2} $$
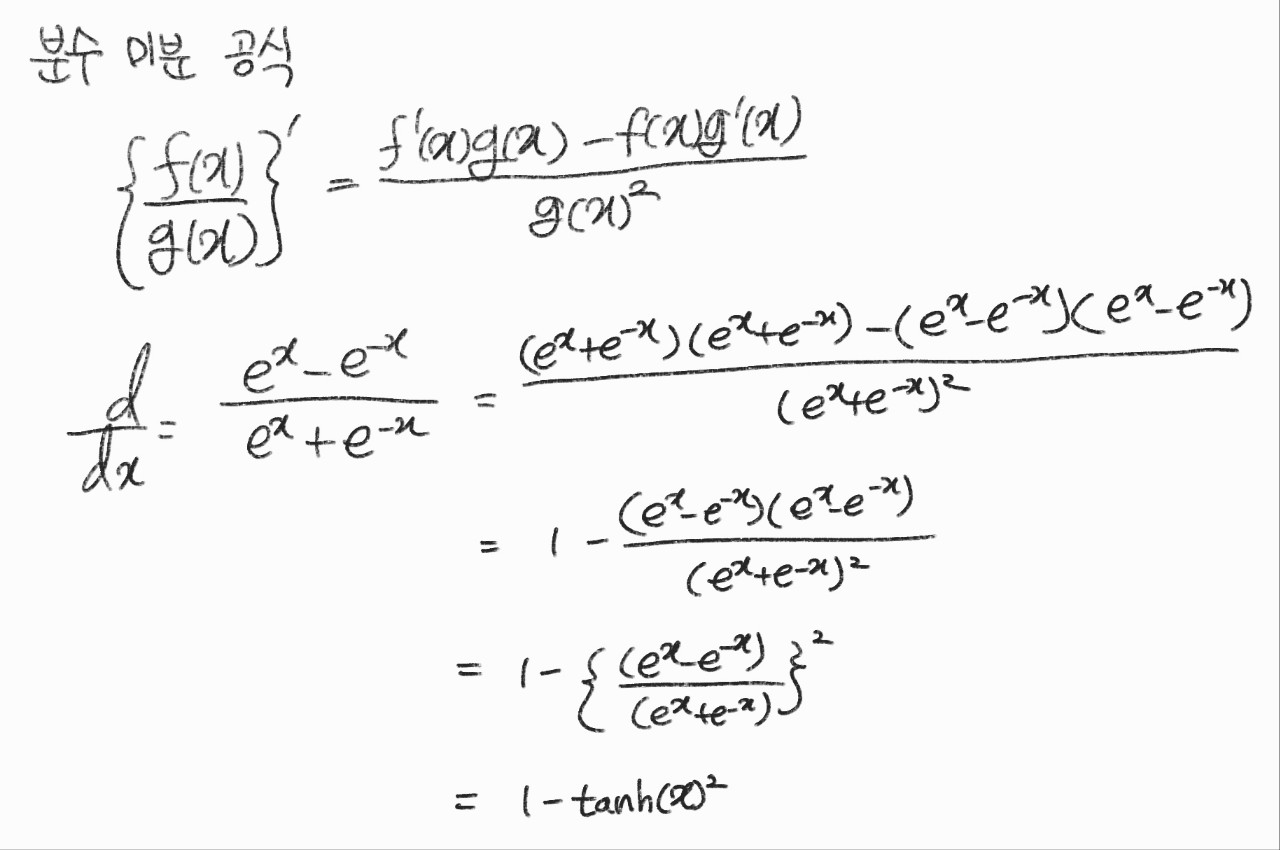


단점
- Sigmoid와 같이 지수 함수가 포함되어 있기 때문에 연산 비용이 많이 든다.
- 그래프를 보면 알 수 있듯 그레디언트 포화 문제를 해결하지 못했다.
구간 선형 함수
ReLU (Rectified Linear Unit) Function
0보다 큰 입력이 들어오면 그대로 통과시키고 0보다 작은 입력이 들어온다면 0을 출력하는 함수이다.
입력값이 0인 경우에만 활성 상태가 됨.
2011년 제프리 힌턴 연구실의 결과에 따르면 sigmoid 계열보다 ReLU 계열이 학습 성능이 좋다고 한다.
$$ ReLU(x)=\begin{cases} & \text{ if } x \geq 0=x\\ & \text{ if } x<0=0 \\ \end{cases} $$


장점
- 연산이 거의 없기 때문에 속도가 빠르다. (음수 구간의 데이터가 0이 되면서 데이터가 Sparse해져서 추가 연산량이 줄어든다.)
- 미분을 계산할 필요가 없기에 속도가 빠르다. (양의 구간 미분 = 1, 음의 구간 미분 = 0)
- 따라서 sigmoid 계열보다 약 6배가 빠르며 양수 구간이 선형 함수 이기 때문에 그레이디언트 소실이 생기지 않는다.
단점
- 양수만 출력하기 때문에 학습 경로가 진동하면서 학습 속도가 느려진다.
- 죽은 ReLU가 발생하면 학습이 진행되지 않을 수 있다.
죽은 ReLU
- Neuron이 계속 0을 출력하는 상태로 그레이디언트도 0이 되어 더 학습되지 않고 같은 값을 출력하게 된다.
- 이 현상은 가중치 초기화를 잘못하거나, 학습률이 클 때 주로 발생하며 뉴런의 10 ~ 20%가 죽은 ReLU이 되면 학습이 잘 안 된다.

Leaky ReLU, PReLU, ELU Function
죽은 ReLU를 해결하기 위해서는 음수 구간이 0이 되지 않도록 약간의 기울기를 주면 되고 이를 보완하여 만든 함수들이
Leaky ReLU, PReLU, ELU Function 이다.
Leaky ReLU
$$ Leaky ReLU(x) = \begin{cases} & \text{ if } x \geq 0 = x \\ & \text{ if } x < 0= 0.01x \end{cases} $$


단점
- 기울기가 고정되어 있기 때문에 최적의 성능을 내지 못할 수 있기에 기울기를 학습하도록 만든 방식이 PReLU(Parametric ReLU)이다
- PReLU를 사용하면 뉴런 별로 기울기를 학습하므로 성능이 개선된다.
PReLU(Parametric ReLU)
a가 parameter로 변경된다.
$$ PReLU(x) = \begin{cases} & \text{ if } x \geq 0 = x \\ & \text{ if } x < 0= ax \end{cases} $$

위의 2개의 ReLU는 큰 음수값이 들어오면 출력 값이 \( -\infty \)로 발산할 수 있다.
ELU Exponential Linear Unit
음수 구간이 지수 함수이기 때문에 큰 음숫값이 들어와도 커지지 않는다.(노이즈에 민감해지지 않음)
$$ ELU(x)=\begin{cases} & \text{ if } x > 0= x\\ & \text{ if } else=\alpha (e^{x}-1) \end{cases} $$

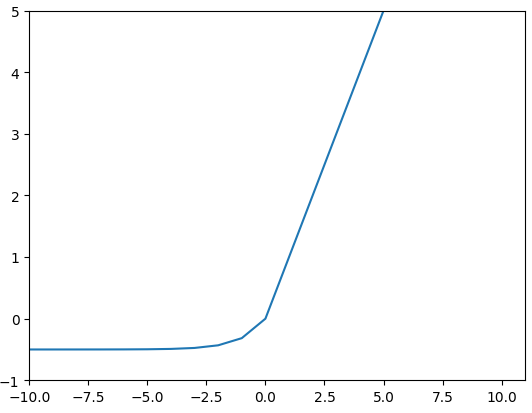
- -\( \alpha \) 까지 천천히 도달함
- log 곡선의 도입으로 The dying ReLU problem 해결함
단점
- 지수 연산이 있기 때문에 계산 시간이 늘어남
- \( \alpha \)값에 대한 학습이 일어나지 않음
- Gradient Exploding이 발생
Maxout
활성 함수도 학습을 통해 얻을 수 있다면 신경망의 성능을 높일 수 있지 않을까?라는 아이디어에서 고안됨
활성 함수를 구간 선형 함수로 가정하고, 각 뉴런에 최적화된 활성 함수를 학습을 통해 찾아낸다.
$$ f(x)=max(W^{T}_{i}x+b_{i}), i =1,2,\cdots ,k $$

Maxout Unit Structure
Maxout 활성 함수를 학습하기 위해 뉴런을 확장한 구조를 Maxout Unit이라고 한다.
맥스 아웃 유닛은 선형 함수를 학습하는 선형 노드와 최댓값을 출력하는 노드로 구성된다.

위의 그림은 맥스 아웃 유닛이 2개 있는 2 계층 신경망이다.
선형 노드 M1, M2, M3와 최댓값을 출력하는 H1노드로 구성되어 있다.
따라서 3개의 선형 함수를 학습하여 세 구간으로 정의되는 구간 선형 함수를 만든다.

Swish Function = SiLU (Sigmoid Linear Unit)
구글 딥러닝 인공지능 연구팀인 Google Brain의 AutoML로 찾은 최적의 활성 함수이다.
원점 근처의 음수 구간에서 볼록 튀어나왔다가 0으로 포화하는 곡선 모양을 가짐
$$ Swish(x) = x\cdot \sigma(x) $$


Differential Swish Function



https://www.v7labs.com/blog/neural-networks-activation-functions
Activation Functions in Neural Networks [12 Types & Use Cases]
A neural network activation function is a function that is applied to the output of a neuron. Learn about different types of activation functions and how they work.
www.v7labs.com
'Machine Learning > 기법' 카테고리의 다른 글
| [ML] 회귀 모델 (0) | 2023.01.04 |
|---|---|
| [ML] 다중 분류 모델 (0) | 2023.01.04 |
| [Optimizer] Adam Adaptive Moment (0) | 2022.08.15 |
| [Optimizer] RMSProp Root Mean Sqaure Propagation (0) | 2022.08.15 |
| [Optimizer] AdaGrad (Adaptive Gradient) (0) | 2022.08.15 |
활성함수 Activation Function

- 신경망에 비선형성을 추가하기 위해 사용함
- 종류
- 이진 활성화 함수 binary step function
- 선형 활성화 함수 linear activation function
- 비선형 활성화 함수 non-linear activation fucntion
- 대부분 비선형 함수를 사용함 (선형 함수를 사용할 경우 역전파가 불가능(도함수가 상수이기 때문) 하고 몇 개를 쌓아도 선형 함수이기 때문에 모든 모델은 선형 회귀 모델로 작동함)
S자형 곡선 함수
Binary Step Function
S형과 유사하지만 곡선 함수는 아님
- \( 0 for X<0 \)
- \( 1 for X>=0 \)



x값을 정수형으로 주어서 그림 2와 같은 그래프가 나왔지만 그림 1과 같은 그래프 형태가 맞음
단점
- multi-class classification 문제에 쓸 수 없음
- 기울기가 0이기 떄문에 오차역전파를 쓸 수 없음
Sigmoid Function
계단 함수와 같이 [0, 1] 범위를 가지고 있다.
모든 구간에서 미분이 가능하고 증가함수이기 때문에 미분값은 항상 양수로 나온다.
$$ \sigma (x) = \frac{1}{1+e^{-x}} $$


Differential Sigmoid function
$$ \frac{d}{dx} sigmoid(x) = sigmoid(x)(1-simoid(x)) $$

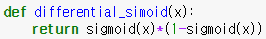

단점
- 지수 함수가 포함되어 있어 연산 비용이 많이 든다.
- 그레디언트 포화가 발생하여 학습이 중단될 수 있다.
- 양수만 출력하기 때문에 학습 경로가 진동하면서 학습 속도가 느려진다.
그레디언트 포화(Gradient saturation)
시그모이드 함수 양 끝 값의 미분값이 0으로 포화되는 상태를 말한다.
함수에서 포화란 입력값이 변화해도 함숫값이 변화하지 않는 상태를 말한다.
이는 기울기 소실(gradient vanishing)로 이어지며 학습이 진행되지 않게 된다.
Tanh(hyperbolic tangent) Function
[-1, 1]의 범위를 가지고 있고 sigmoid 함수의 양수 출력 문제를 해결하고자 고안된 함수이다.
$$ tanh(x) = \frac{e^{x}-e^{-x}}{e^{x}+e^{-x}} $$
Sigmoid의 선형 변환식으로 나타낼 수 있음
$$ tanh(x) = 2\sigma(2x)-1 $$

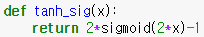

Differential Sigmoid Function
$$ \frac{d}{dx} tanh(x) = 1 - tanh(x)^{2} $$
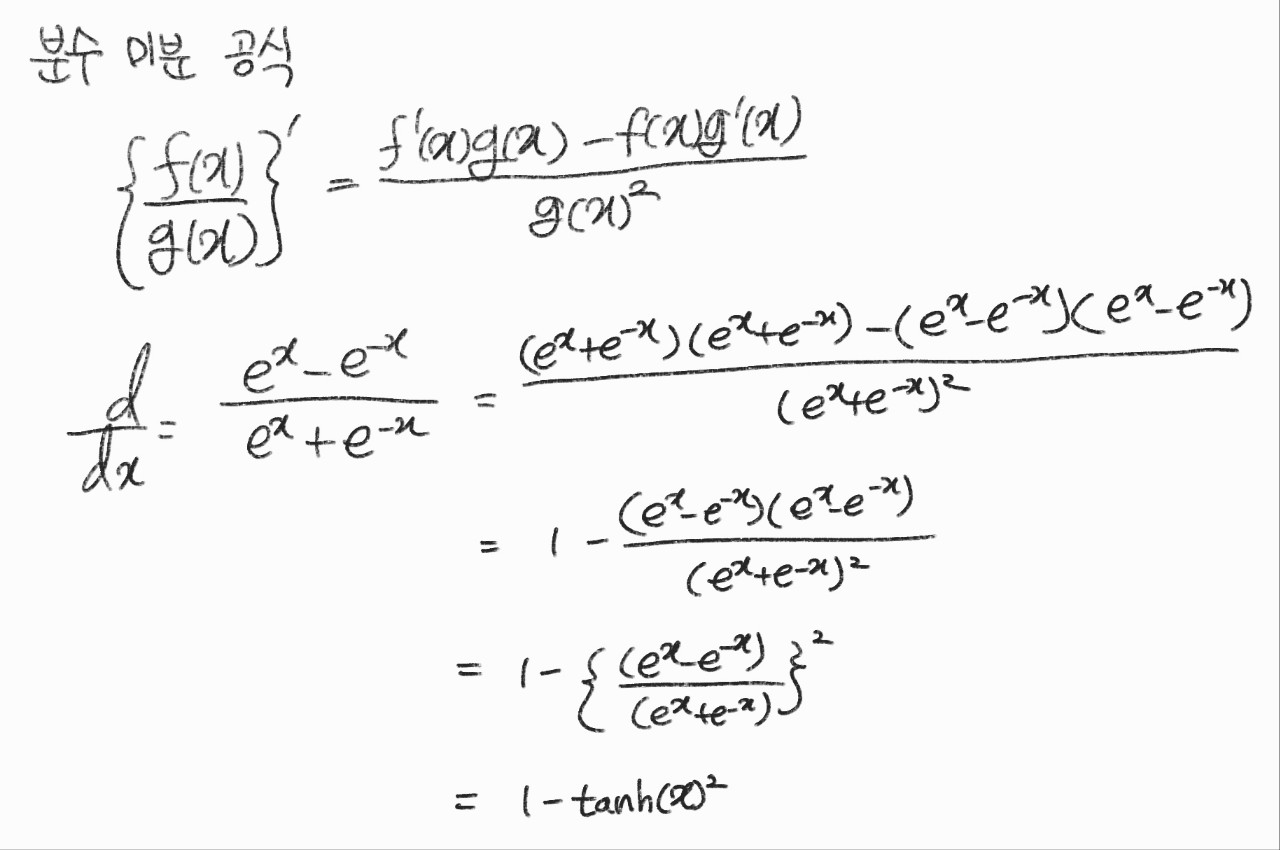


단점
- Sigmoid와 같이 지수 함수가 포함되어 있기 때문에 연산 비용이 많이 든다.
- 그래프를 보면 알 수 있듯 그레디언트 포화 문제를 해결하지 못했다.
구간 선형 함수
ReLU (Rectified Linear Unit) Function
0보다 큰 입력이 들어오면 그대로 통과시키고 0보다 작은 입력이 들어온다면 0을 출력하는 함수이다.
입력값이 0인 경우에만 활성 상태가 됨.
2011년 제프리 힌턴 연구실의 결과에 따르면 sigmoid 계열보다 ReLU 계열이 학습 성능이 좋다고 한다.
$$ ReLU(x)=\begin{cases} & \text{ if } x \geq 0=x\\ & \text{ if } x<0=0 \\ \end{cases} $$


장점
- 연산이 거의 없기 때문에 속도가 빠르다. (음수 구간의 데이터가 0이 되면서 데이터가 Sparse해져서 추가 연산량이 줄어든다.)
- 미분을 계산할 필요가 없기에 속도가 빠르다. (양의 구간 미분 = 1, 음의 구간 미분 = 0)
- 따라서 sigmoid 계열보다 약 6배가 빠르며 양수 구간이 선형 함수 이기 때문에 그레이디언트 소실이 생기지 않는다.
단점
- 양수만 출력하기 때문에 학습 경로가 진동하면서 학습 속도가 느려진다.
- 죽은 ReLU가 발생하면 학습이 진행되지 않을 수 있다.
죽은 ReLU
- Neuron이 계속 0을 출력하는 상태로 그레이디언트도 0이 되어 더 학습되지 않고 같은 값을 출력하게 된다.
- 이 현상은 가중치 초기화를 잘못하거나, 학습률이 클 때 주로 발생하며 뉴런의 10 ~ 20%가 죽은 ReLU이 되면 학습이 잘 안 된다.

Leaky ReLU, PReLU, ELU Function
죽은 ReLU를 해결하기 위해서는 음수 구간이 0이 되지 않도록 약간의 기울기를 주면 되고 이를 보완하여 만든 함수들이
Leaky ReLU, PReLU, ELU Function 이다.
Leaky ReLU
$$ Leaky ReLU(x) = \begin{cases} & \text{ if } x \geq 0 = x \\ & \text{ if } x < 0= 0.01x \end{cases} $$


단점
- 기울기가 고정되어 있기 때문에 최적의 성능을 내지 못할 수 있기에 기울기를 학습하도록 만든 방식이 PReLU(Parametric ReLU)이다
- PReLU를 사용하면 뉴런 별로 기울기를 학습하므로 성능이 개선된다.
PReLU(Parametric ReLU)
a가 parameter로 변경된다.
$$ PReLU(x) = \begin{cases} & \text{ if } x \geq 0 = x \\ & \text{ if } x < 0= ax \end{cases} $$

위의 2개의 ReLU는 큰 음수값이 들어오면 출력 값이 \( -\infty \)로 발산할 수 있다.
ELU Exponential Linear Unit
음수 구간이 지수 함수이기 때문에 큰 음숫값이 들어와도 커지지 않는다.(노이즈에 민감해지지 않음)
$$ ELU(x)=\begin{cases} & \text{ if } x > 0= x\\ & \text{ if } else=\alpha (e^{x}-1) \end{cases} $$


- -\( \alpha \) 까지 천천히 도달함
- log 곡선의 도입으로 The dying ReLU problem 해결함
단점
- 지수 연산이 있기 때문에 계산 시간이 늘어남
- \( \alpha \)값에 대한 학습이 일어나지 않음
- Gradient Exploding이 발생
Maxout
활성 함수도 학습을 통해 얻을 수 있다면 신경망의 성능을 높일 수 있지 않을까?라는 아이디어에서 고안됨
활성 함수를 구간 선형 함수로 가정하고, 각 뉴런에 최적화된 활성 함수를 학습을 통해 찾아낸다.
$$ f(x)=max(W^{T}_{i}x+b_{i}), i =1,2,\cdots ,k $$

Maxout Unit Structure
Maxout 활성 함수를 학습하기 위해 뉴런을 확장한 구조를 Maxout Unit이라고 한다.
맥스 아웃 유닛은 선형 함수를 학습하는 선형 노드와 최댓값을 출력하는 노드로 구성된다.

위의 그림은 맥스 아웃 유닛이 2개 있는 2 계층 신경망이다.
선형 노드 M1, M2, M3와 최댓값을 출력하는 H1노드로 구성되어 있다.
따라서 3개의 선형 함수를 학습하여 세 구간으로 정의되는 구간 선형 함수를 만든다.

Swish Function = SiLU (Sigmoid Linear Unit)
구글 딥러닝 인공지능 연구팀인 Google Brain의 AutoML로 찾은 최적의 활성 함수이다.
원점 근처의 음수 구간에서 볼록 튀어나왔다가 0으로 포화하는 곡선 모양을 가짐
$$ Swish(x) = x\cdot \sigma(x) $$


Differential Swish Function



https://www.v7labs.com/blog/neural-networks-activation-functions
Activation Functions in Neural Networks [12 Types & Use Cases]
A neural network activation function is a function that is applied to the output of a neuron. Learn about different types of activation functions and how they work.
www.v7labs.com
'Machine Learning > 기법' 카테고리의 다른 글
| [ML] 회귀 모델 (0) | 2023.01.04 |
|---|---|
| [ML] 다중 분류 모델 (0) | 2023.01.04 |
| [Optimizer] Adam Adaptive Moment (0) | 2022.08.15 |
| [Optimizer] RMSProp Root Mean Sqaure Propagation (0) | 2022.08.15 |
| [Optimizer] AdaGrad (Adaptive Gradient) (0) | 2022.08.15 |
