이진 분류 모델
동전 던지기를 할 때 앞면과 뒷면이 나올 확률을 예측하는 문제와 같음
앞면, 뒷면이 나올 확률은 베르누이 분포(Bernoulli Distribution)로 정의 되기에, 이진 분류 모델은 베르누이 분포를 예측하는 모델로 정의할 수 있다.
베르누이 분포 Bernoulli Distribution
두 종류의 사건이 발생할 확률
$$ p(x; \mu ) = \mu^{x}(1-\mu)^{1-x}, x \in \{0,1\} $$
x는 확률 변수로 x = 1 이면 사건 1을 나태내고, x = 0 이면 사건 2를 나타낸다.
\( \mu \)는 사건 1이 발생할 확률, \( 1-\mu \)는 사건 2가 발생할 확률이다.
$$ p(x = 1; \mu ) = \mu = \frac{1}{2} $$
$$ p(x = 0; \mu ) = 1-\mu = \frac{1}{2} $$
확률 모델 정의
관측데이터(Dataset)는 \( \mathbb{D} = \{ (x_{i}, t_{i}): i = 1, \ldots ,N \} \) 로 N개의 \( (x_{i}, t_{i} \) 샘플로 구성되며, 입력 데이터는 \( x_{i} \)는 같은 분포에서 독립적으로 샘플링되어 i.i.d를 만족한다고 하자.
\( t_{i} \) 가 1 이면 class는 1, 0이면 class는 2이다.
이진 분류 모델은 타깃 \( t_{i} \)의 확률 분포인 베르누이 분포의 파라미터 \( \mu \)를 예측한다.
모델은 입력으로 \( x_{i} \)를 받았을 때 분포 파라미터에 \( \mu \)에 해당하는 \( \mu(x_{i}; \theta) \)를 출력한다.
그 결과 다음과 같은 베르누이 분포를 예측할 수 있음
$$ p(t_{i}|x_{i}; \theta) = Bern (t_{i}; \mu(x_{i};\theta)) = \mu(x_{i} ; \theta)^{t_{i}}(1-\mu(x_{i};\theta))^{1-t_{i}} $$

출력 계층의 활성 함수
모델이 \( \mu \)(확률)를 예측할 때 점수(Score) 또는 로짓 (Logit)으로 예측하고 이를 활성 함수를 통해 베르누이 확률분포의 파라미터 \( \mu \)로 변환한다. 이때 사용하는 활성화 함수는 Sigmoid 함수이다.
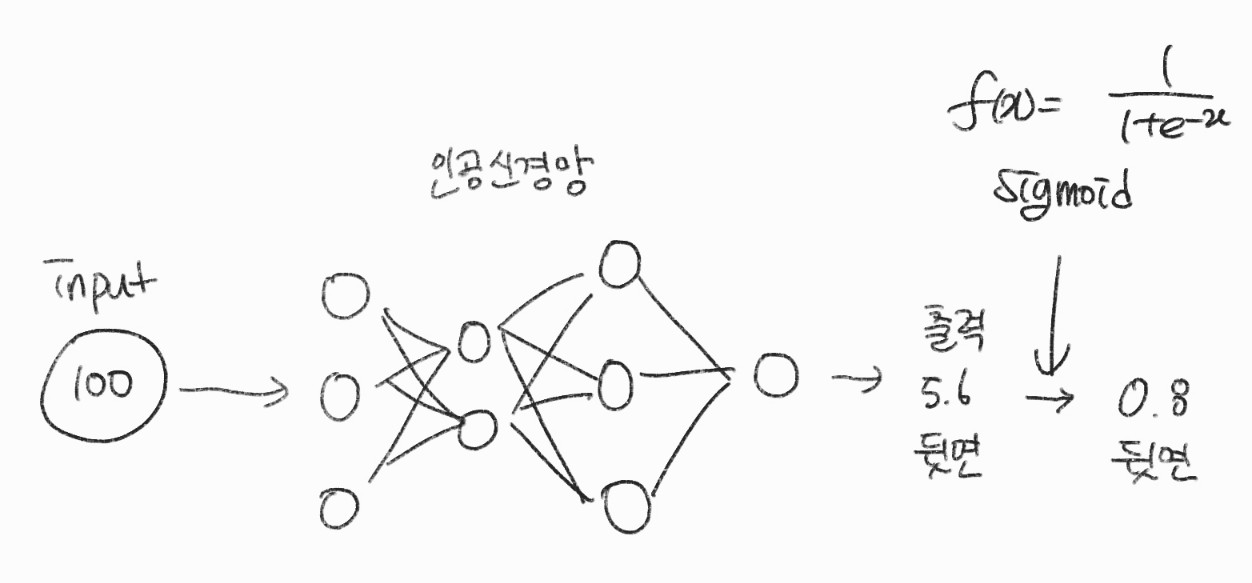
이진 분류 모델의 결과가 확률로 출력되기 때문에 입력 데이터를 어떤 클래스로 분류할지는 결정 경계를 정하기 나름이다.
logit
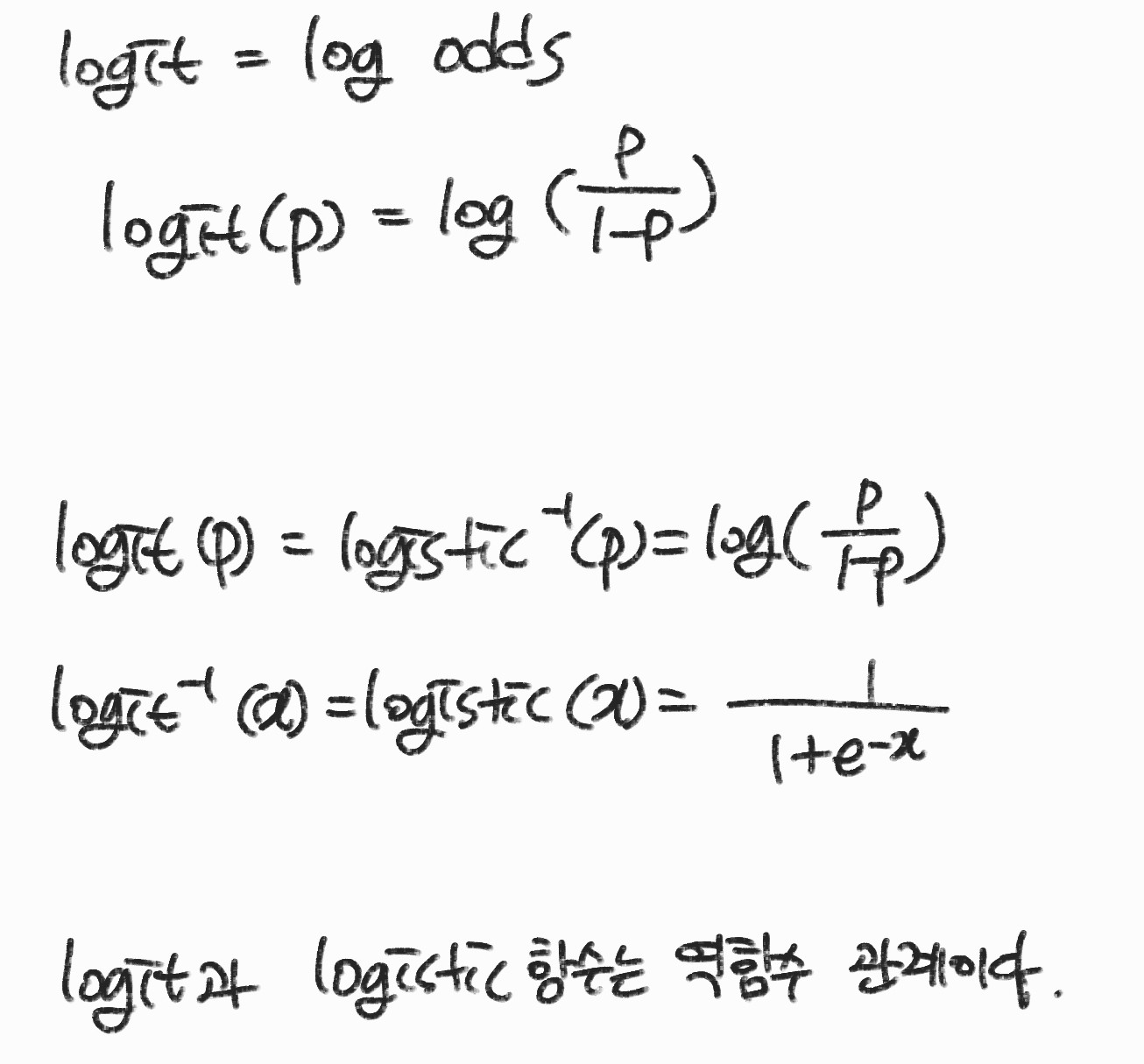
'Machine Learning > Model' 카테고리의 다른 글
| [ML] KNN(K-Nearest Neighborhood), k-최근접 이웃 (0) | 2023.03.22 |
|---|---|
| [ML] 나이브 베이즈(Naive bayes) 개념, 실습 (0) | 2023.03.21 |
| [ML] 순방향 신경망(FNN), 신경망의 설계 (0) | 2023.01.03 |
| [DATA] Custom Image Data 넣기 (0) | 2022.12.28 |
| [CNN] CNN Stride (Convolution Neural Network) (0) | 2022.09.29 |
