회귀 분석
- 독립변수와 종속변수 사이의 함수적 관계를 구하는데 사용되는 것
- 선형과 비선형이 있음
단순 선형 회귀 분석
- 한 개의 독립변수와 한 개의 종속 변수 사이의 함수적 관계를 선형으로 분석하는 것
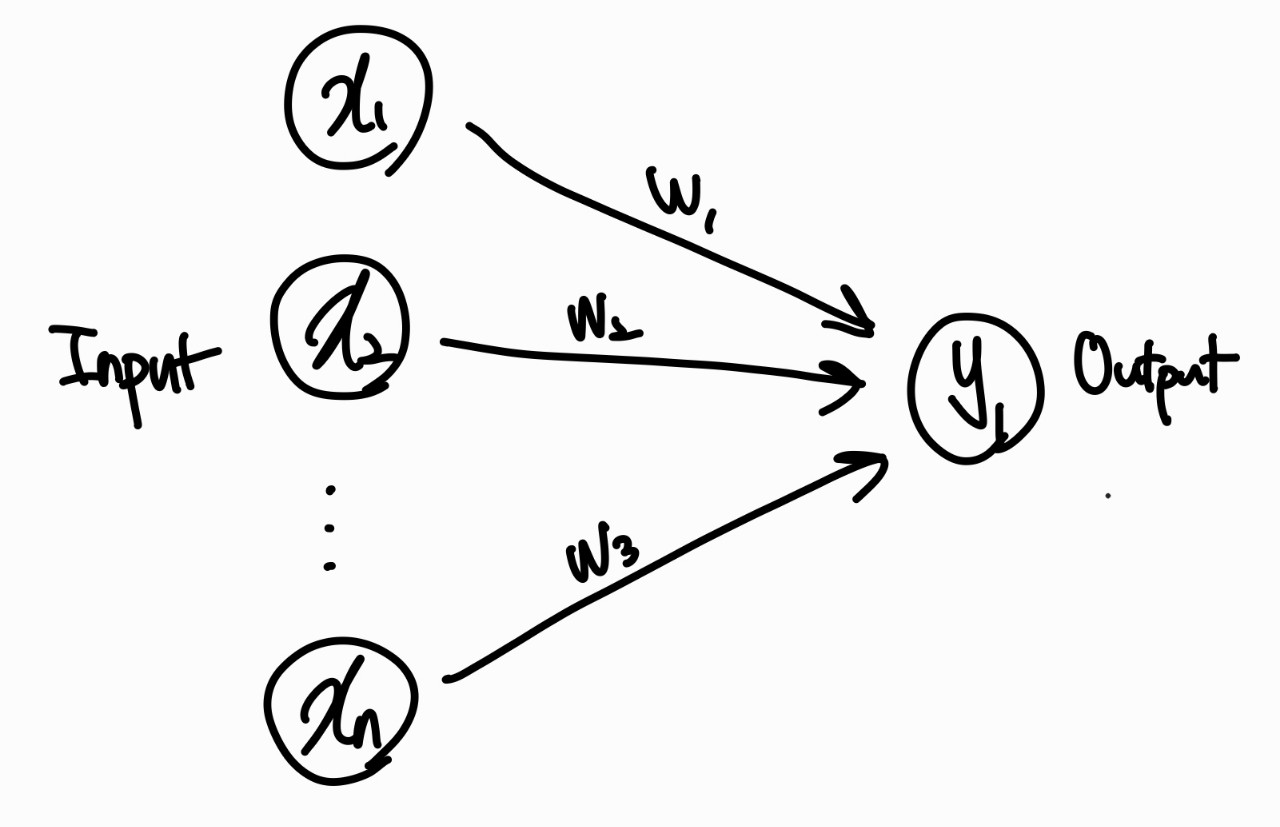
독립변수 Independent Variable : 독립적으로 변하는 값 (\( x \)값)
종속변수 Dependent Variable : 독립변수에 따라 변하는 값 (\( y \) 값)
다중 선형 회귀 분석
- 두 개 이상의 독립변수와 한 개의 종속변수 사이의 함수적 관계 선형으로 분석하는 것
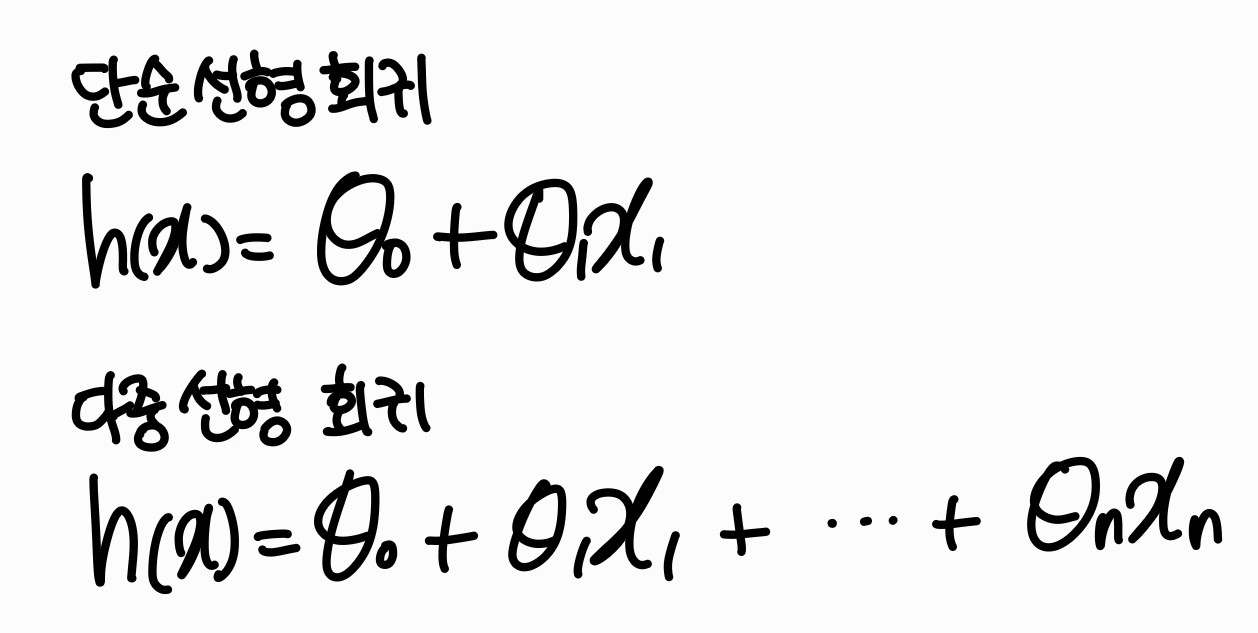
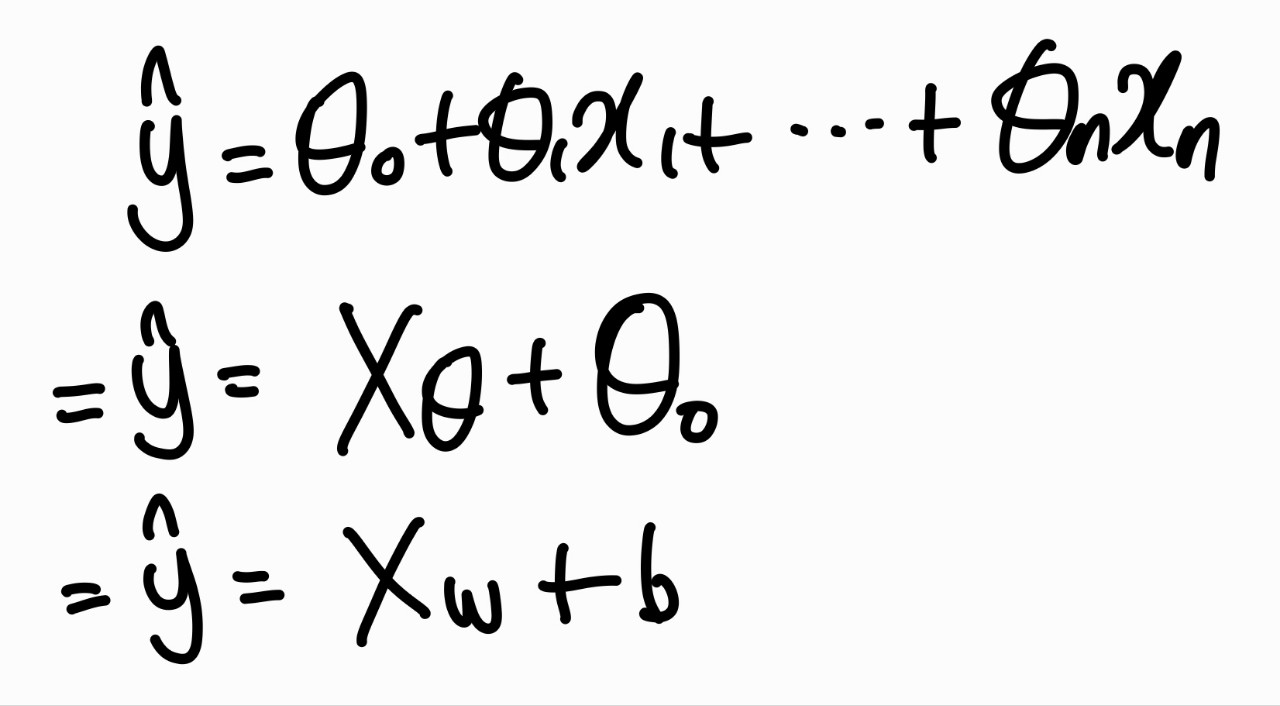
다중 선형 회귀의 Loss function
- 다중 선형 회귀의 오류를 측정하는 함수
$$ l^{(i)}(W,b) = \frac{1}{2}( \hat{y}^{(i)}-y^{(i)})^{2} $$
$$ L(W,b) = \frac{1}{n} \sum_{i=1}^n (W,b) = \frac{1}{n} \sum_{i=1}^n \frac{1}{2}(W^{T}x^{(i)}+b-y^{(i)})^{2} $$
$$ W^{*}, b^{*} = argmin L(W,b) $$
경사하강법
https://pasongsong.tistory.com/5
인공지능 - 경사 하강법
선형 회귀에서 잠깐 말했었던 예측선을 수정하는 걸 해볼 것이다. a값을 무한대로 키우거나 작게 하면 오차는 무한대로 커진다. 이러한 관계를 이차 함수 그래프로 표현이 가능하다. 이걸 이용
pasongsong.tistory.com
다중 선형 회귀로 적절한 w 구하는 방법
가중치 벡터(T) 와 독립변수 벡터를 만들고 이를 행렬의 곱을 하여 \( \hat{y} \)를 구한다.
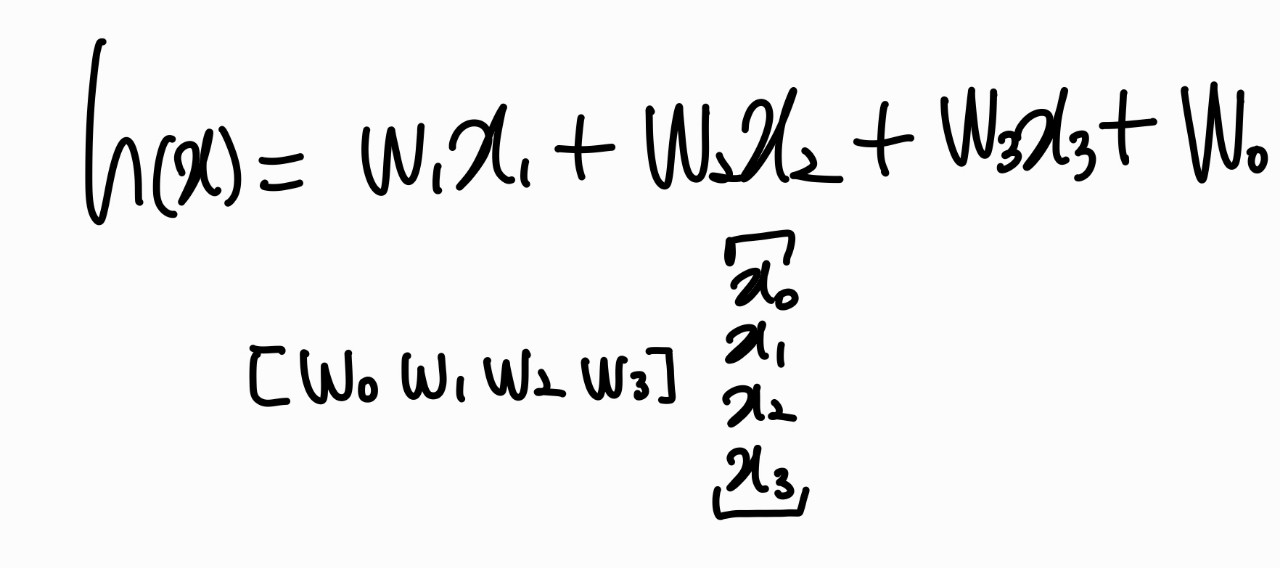
Loss Function을 이용하여 현재 \( w^{*}, b^{*} \)가 잘 학습되었는지 확인한다.
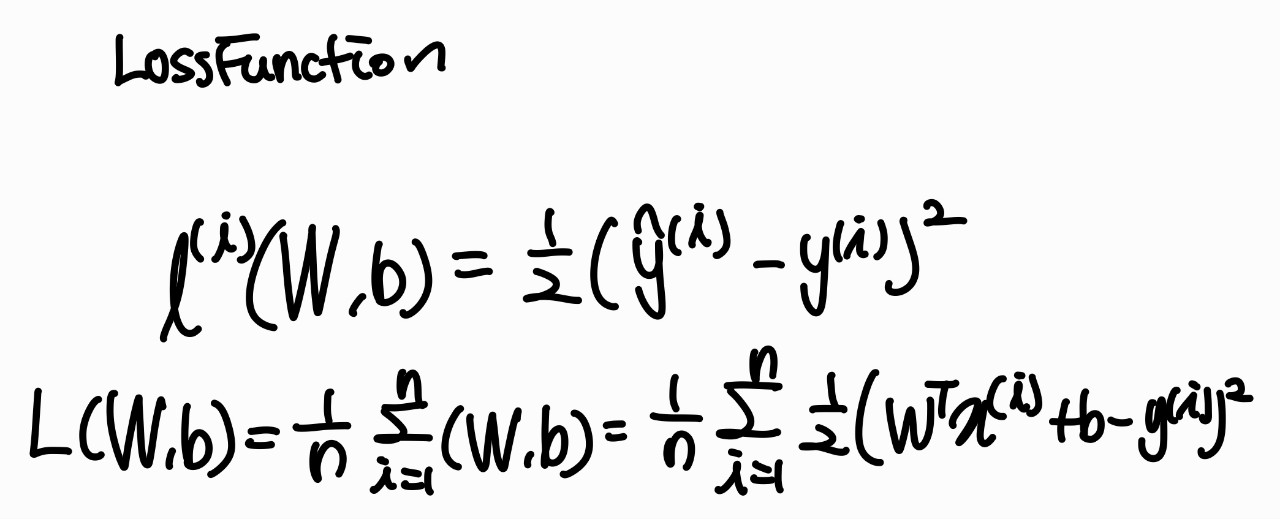
\( w^{*}, b^{*} \) 구하는 방법
경사하강법을 이용한다. (평균 제곱 오차 MSE를 사용한다. \( \frac{1}{n} \sum (\hat{y_{i}}-y_{i})^{2} \) )

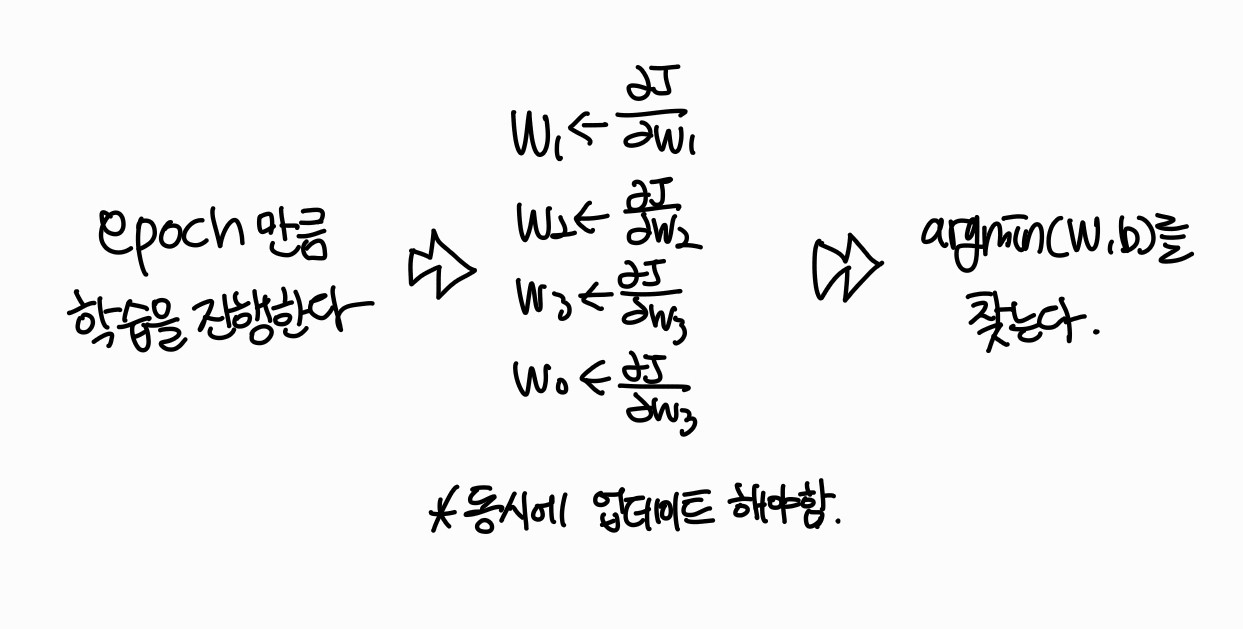
argmin W, b를 구하기 위해서 argmin(W, b)가 나올때까지 미분값을 빼면서 W, b를 업데이트 시켜야한다.

각각의 편미분 값을 빼주면서 모델을 학습시킨다
정리!
'Machine Learning > 이론' 카테고리의 다른 글
| [ML] Neural Network (0) | 2022.09.27 |
|---|---|
| [ML] 오차역전파 Backpropagation (0) | 2022.09.04 |
| [ML] 교차 검증 Cross Validatoin (0) | 2022.08.22 |
| [ML] 규제 Regularization (0) | 2022.08.18 |
| [ML] Overfitting 막는 방법 (0) | 2022.08.17 |
