-
오차역전파
-
1. 손실 함수 미분
-
2. 출력 뉴런 미분
-
3. 은닉 계층 미분 전달
-
Unit의 오차
-
\( \frac{\partial C}{\partial z_{1}^{2}}\frac{\partial z_{1}^{2}}{\partial w_{11}^{2}} \) 을 \( \delta_{j}^{l} \)으로 표현하기
-
\( \delta_{j}^{l} \) 일반화 하기
-
오차역전파
-
출력층의 \( \delta_{j}^{l} \) 계산
-
은닉층 \( \delta_{j}^{l} \) '역' 점화식
-
일반화 \( \delta_{j}^{l} \delta_{j}^{l+1} \) 관계
-
\( w_{11}^{2} \) 갱신
오차역전파
경사 하강법의 방법으로 손실 함수에서 가중치까지 신경망의 역방향으로 실행하면 시간이 오래 걸리고 비효율성 문제가 생긴다.
이를 해결하기 위해 오차 역전파 알고리즘(Back Propagation Algorithm)이다.

공통부분은 한 번 계산해두면 같은 뉴런에 속한 모든 가중치의 미분을 계산할 때 재사용할 수 있다.
1. 손실 함수 미분
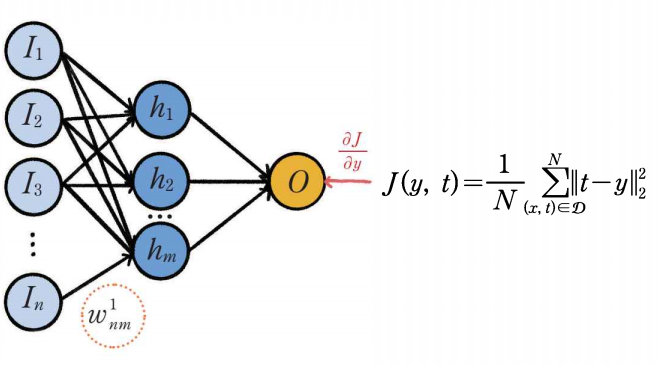
손실 함수 전역 미분 \( \frac{\partial J}{\partial y} \)을 출력 계층 \( O \)에 전달한다.
2. 출력 뉴런 미분
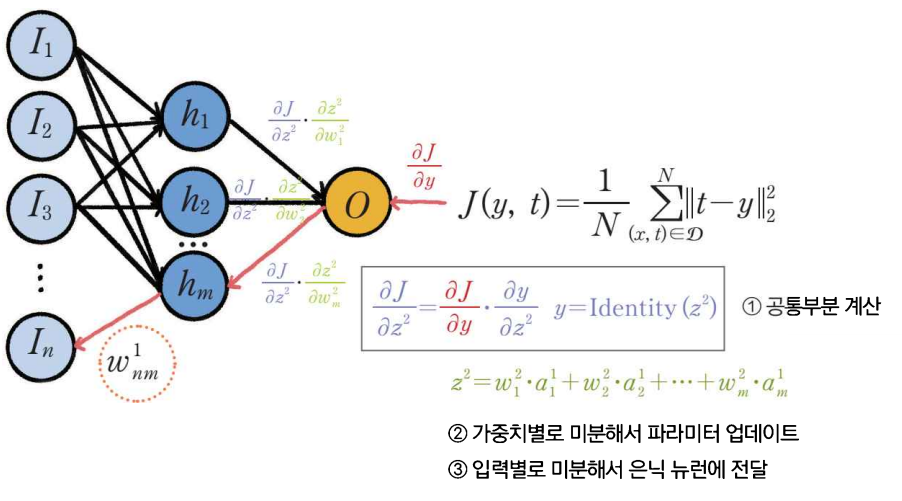
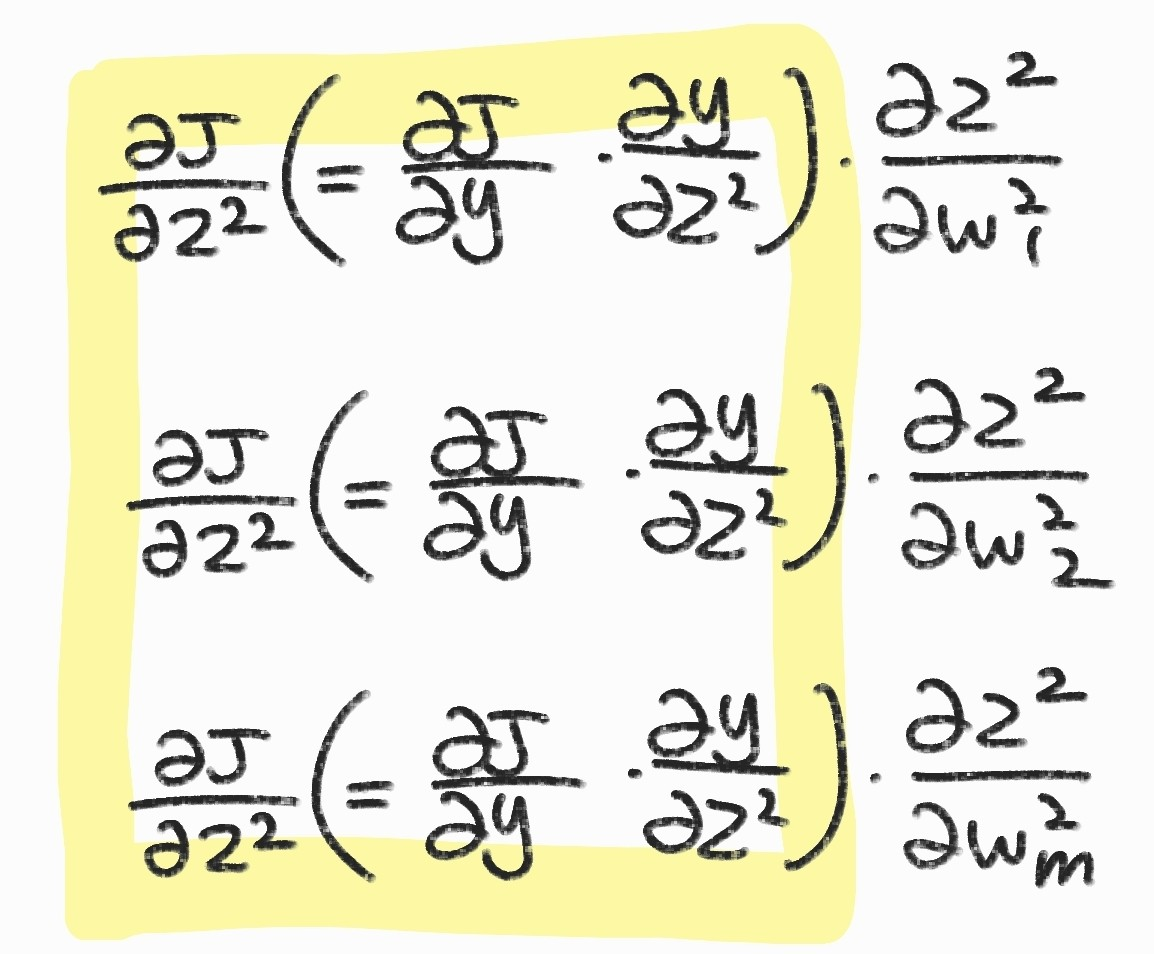
공통부분 계산
활성 함수 지역 미분: \( \frac{\partial y}{\partial z^{2}} \)
활성 함수 전역 미분 : \( \frac{\partial J}{\partial y} \) 와 \( \frac{\partial y}{\partial z^{2}} \)를 곱해서 활성 합수 전역 미분 \( \frac{\partial J}{\partial z^{2}} \)를 계산한다.
가중치 업데이트

은닉 계층에 미분 전달

3. 은닉 계층 미분 전달
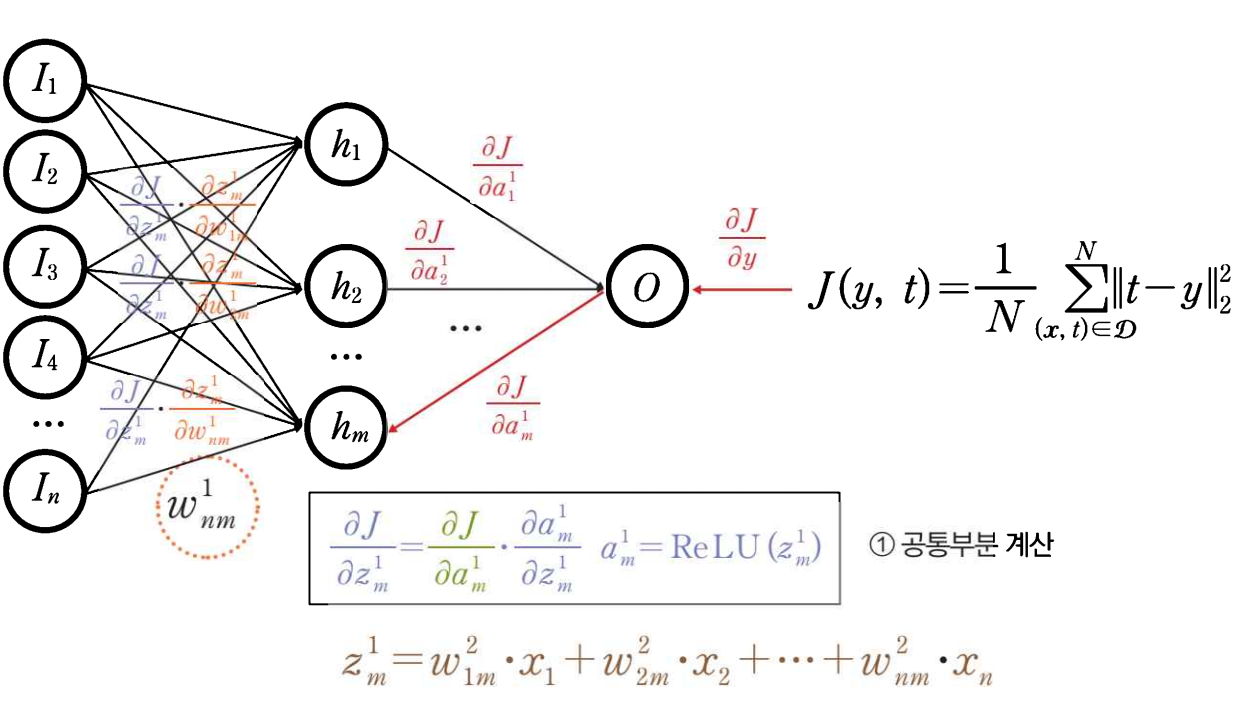
Unit의 오차
- Unit의 가중 입력 \( z_{j}^{l} \)이 제곱오차에 미치는 변화율
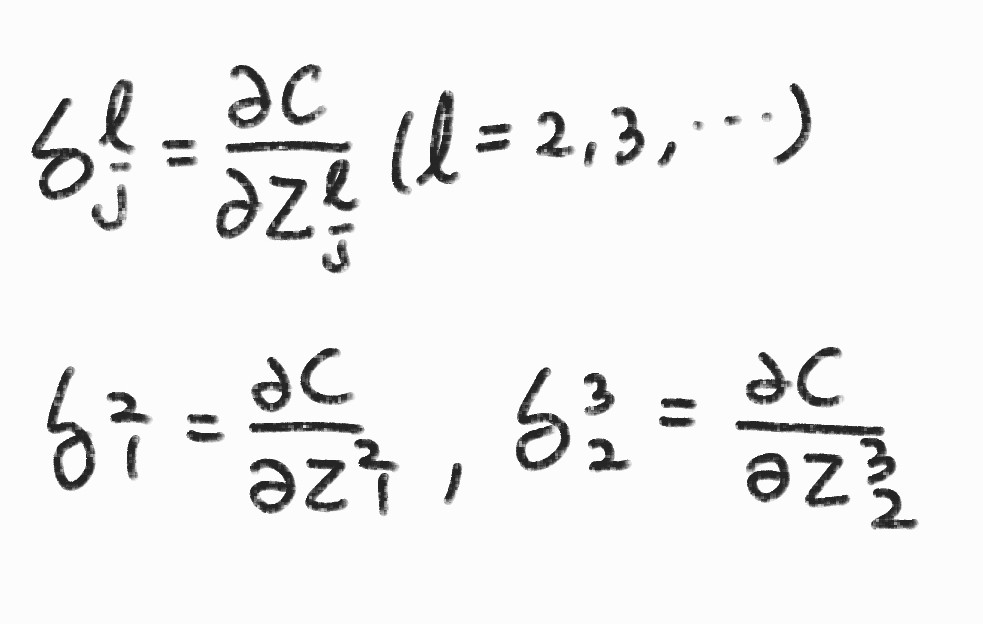
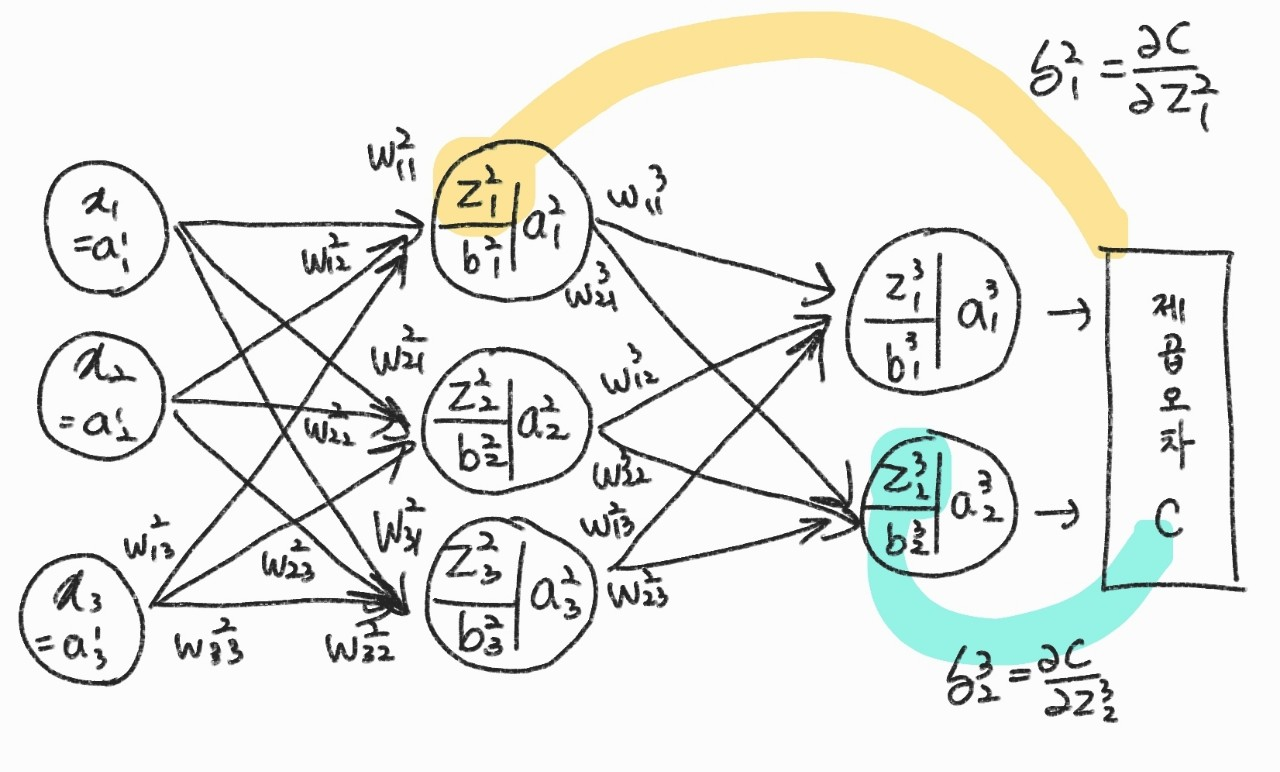
\( \frac{\partial C}{\partial z_{1}^{2}}\frac{\partial z_{1}^{2}}{\partial w_{11}^{2}} \) 을 \( \delta_{j}^{l} \)으로 표현하기
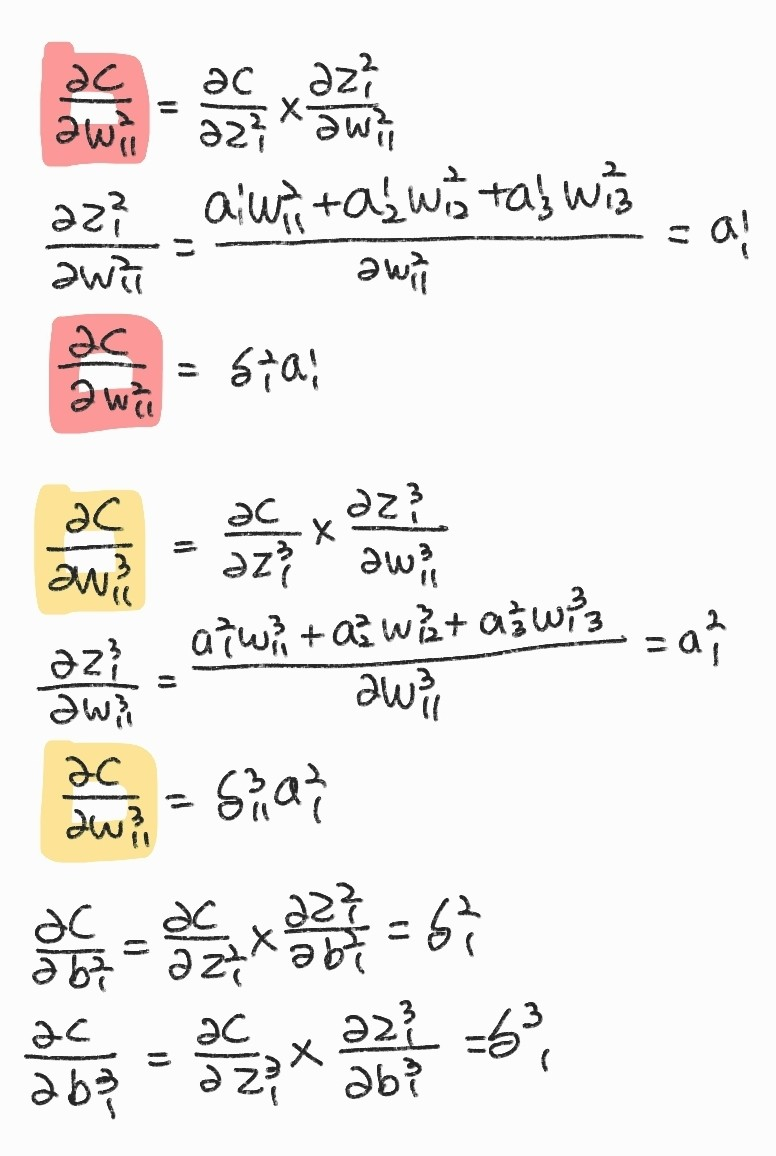
\( \delta_{j}^{l} \) 일반화 하기
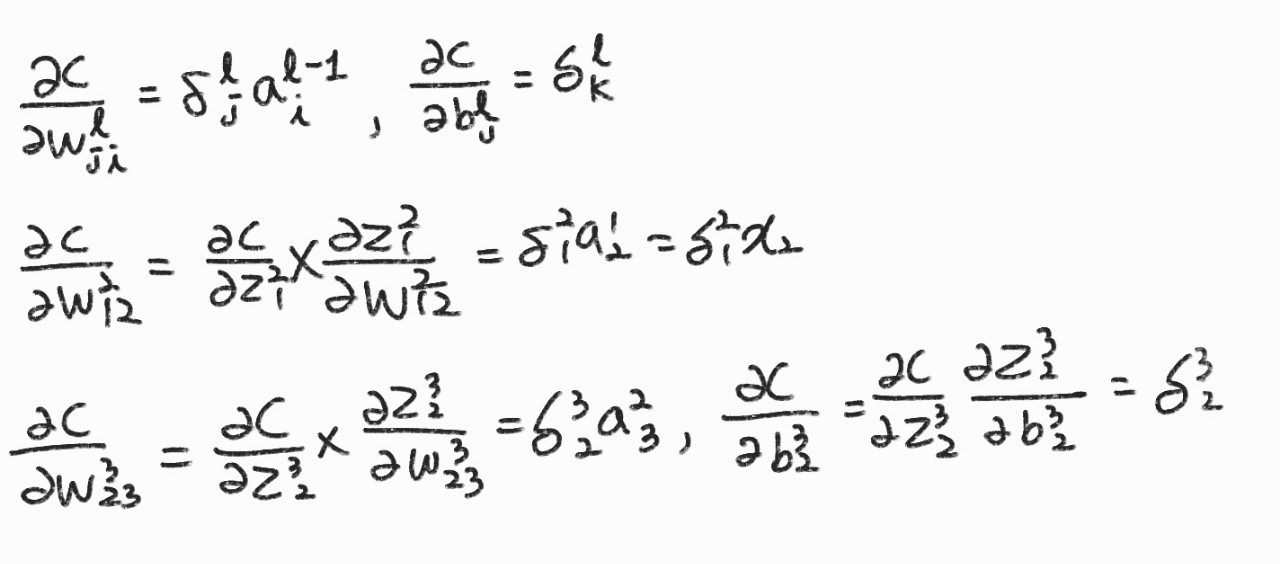
오차역전파
- \( \delta_{j}^{l} \)를 정의하는 방법( \( l \)층 \( j \) 번째)
- Multi layer perceptron을 학습시키기 위한 방법
- Output layer에서의 error의 변화량을 앞선 layer들로 전파하는 방법
- 미분을 통하여 접근함
출력층의 \( \delta_{j}^{l} \) 계산


은닉층 \( \delta_{j}^{l} \) '역' 점화식
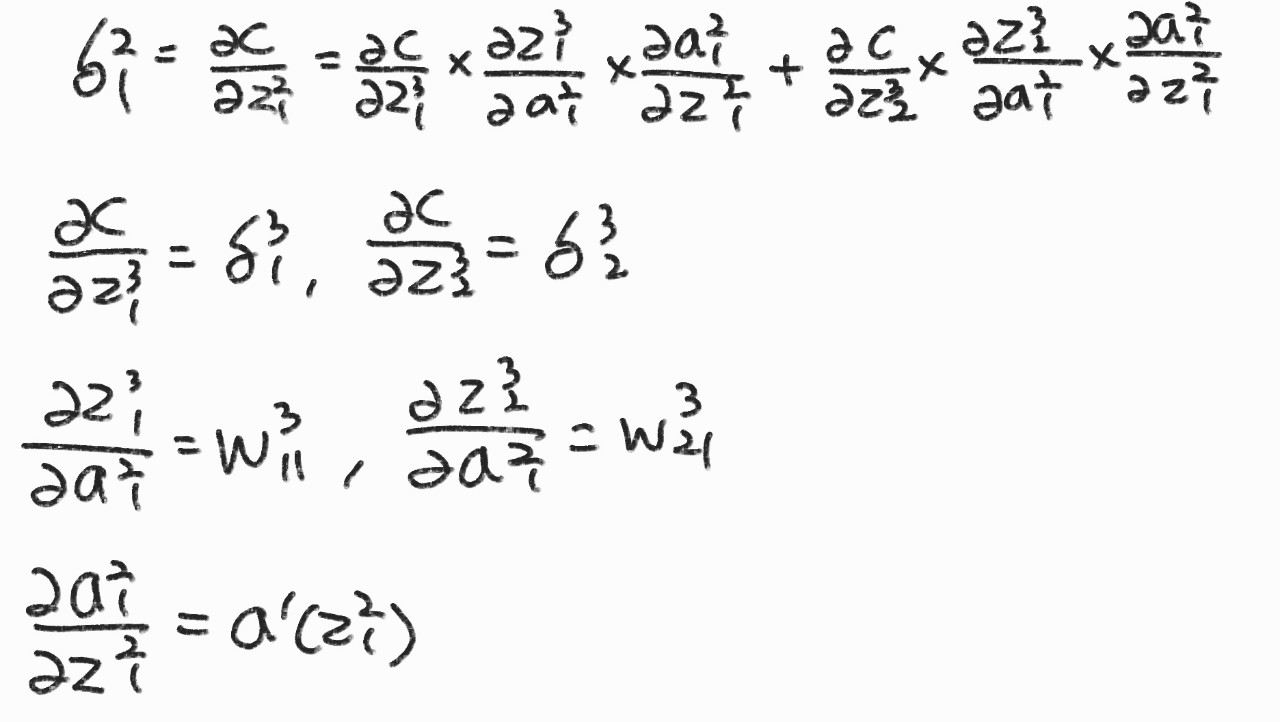
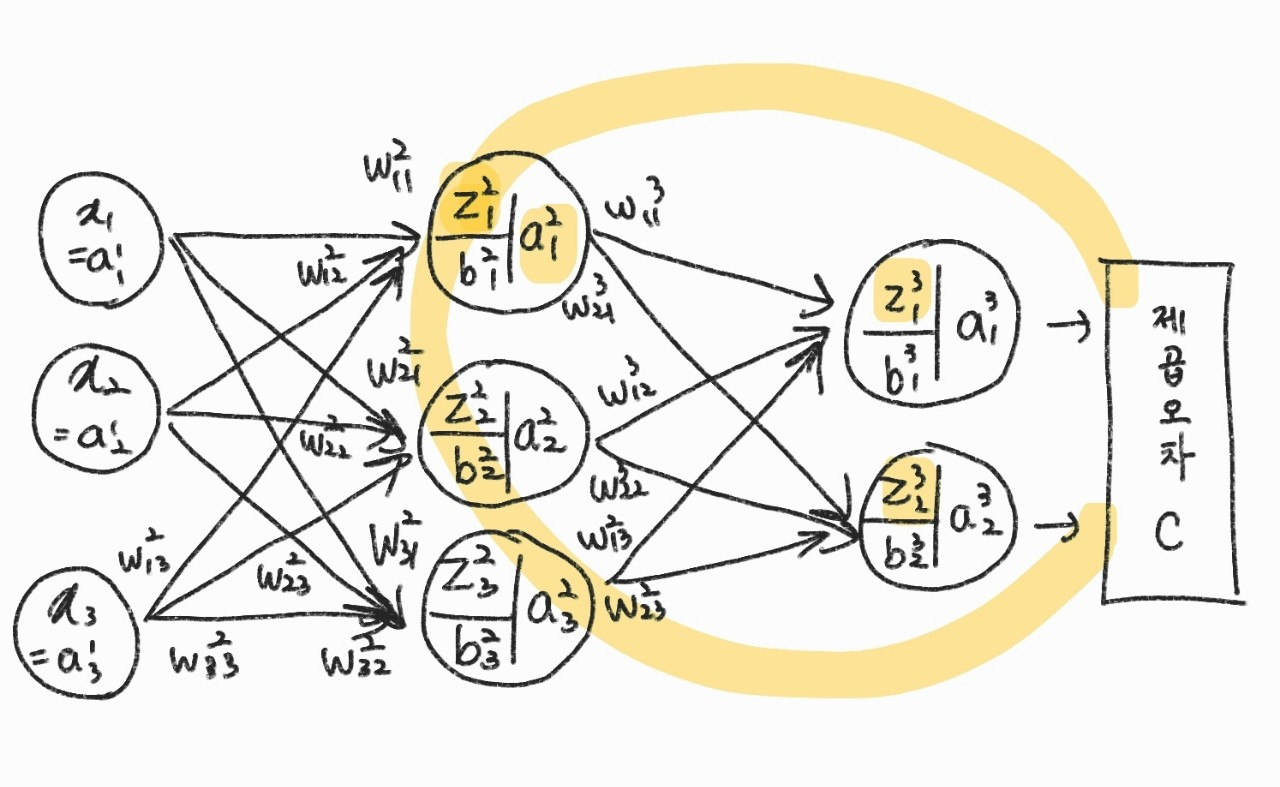
일반화 \( \delta_{j}^{l} \delta_{j}^{l+1} \) 관계
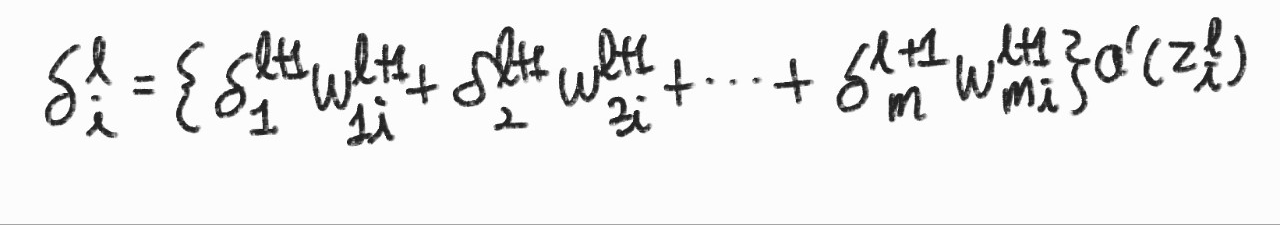
\( w_{11}^{2} \) 갱신
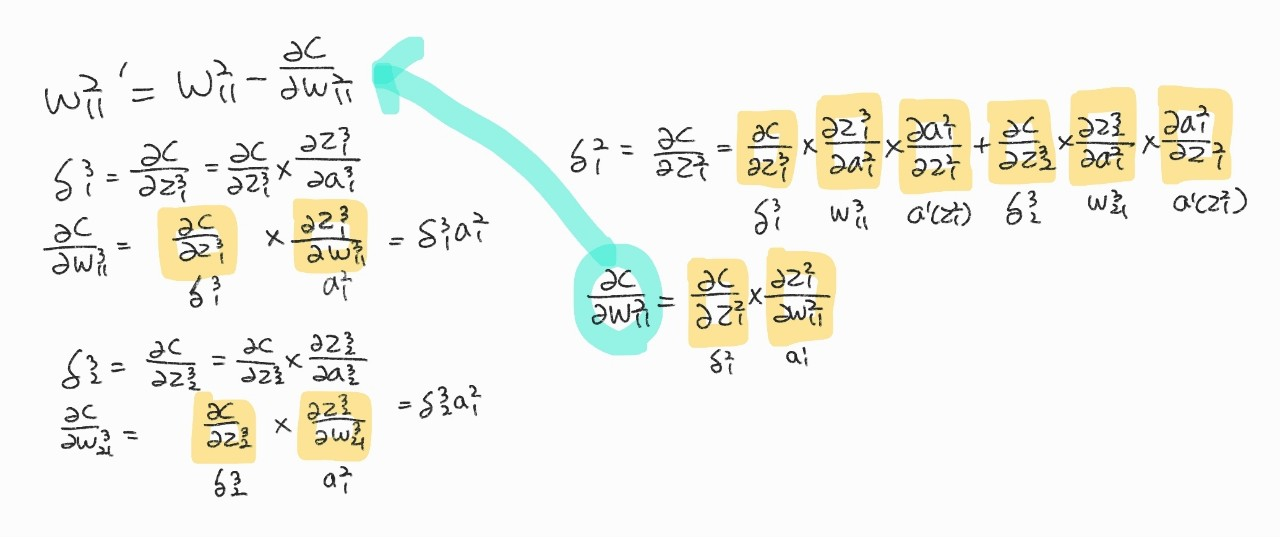
출력층 유닛의 오차만으로 다른 유닛의 오차를 미분없이 구할 수 있음
이것이 오차역전파!
'Machine Learning > 이론' 카테고리의 다른 글
| [ML] Image data (0) | 2022.09.29 |
|---|---|
| [ML] Neural Network (0) | 2022.09.27 |
| [ML] 회귀 분석 (Regression Analysis) (0) | 2022.08.27 |
| [ML] 교차 검증 Cross Validatoin (0) | 2022.08.22 |
| [ML] 규제 Regularization (0) | 2022.08.18 |
오차역전파
경사 하강법의 방법으로 손실 함수에서 가중치까지 신경망의 역방향으로 실행하면 시간이 오래 걸리고 비효율성 문제가 생긴다.
이를 해결하기 위해 오차 역전파 알고리즘(Back Propagation Algorithm)이다.

공통부분은 한 번 계산해두면 같은 뉴런에 속한 모든 가중치의 미분을 계산할 때 재사용할 수 있다.
1. 손실 함수 미분

손실 함수 전역 미분 \( \frac{\partial J}{\partial y} \)을 출력 계층 \( O \)에 전달한다.
2. 출력 뉴런 미분

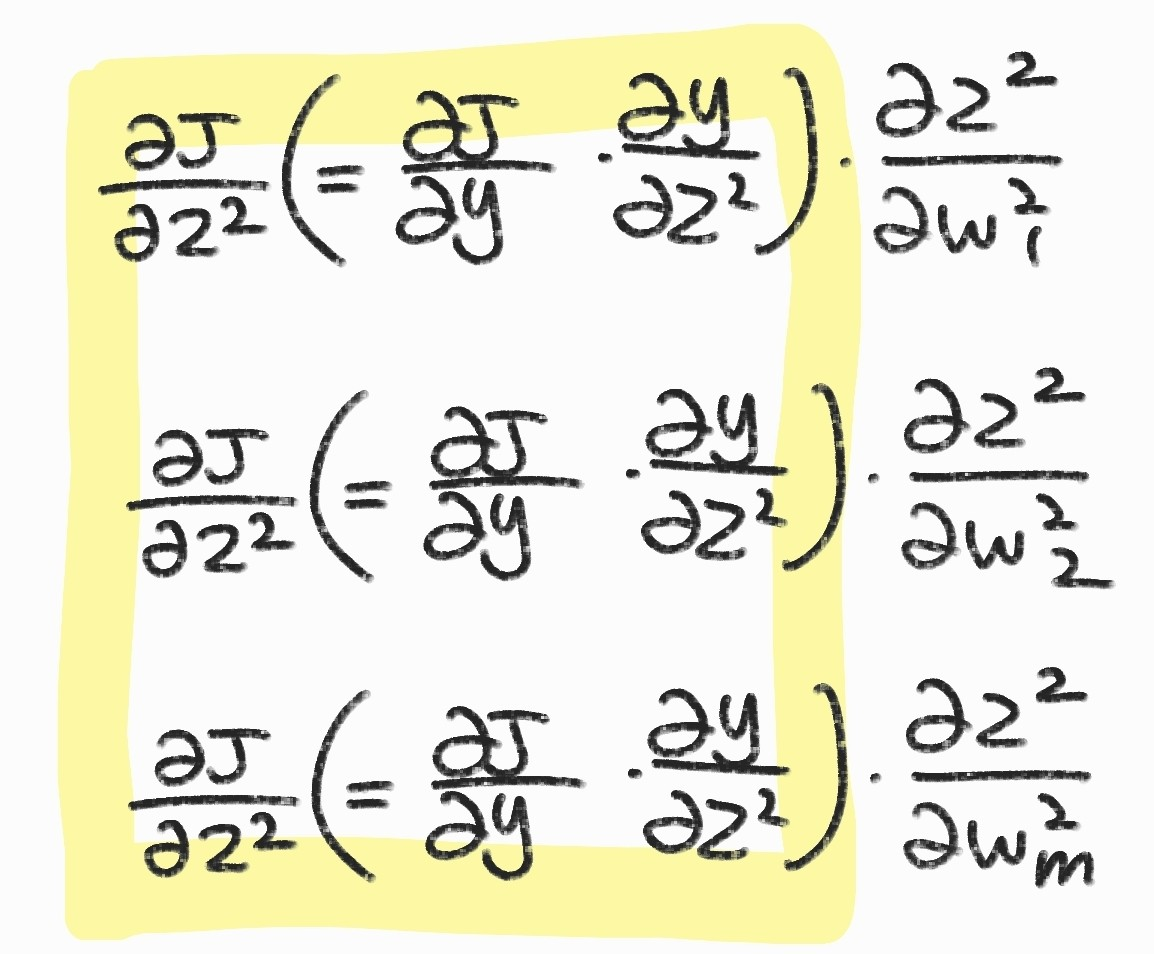
공통부분 계산
활성 함수 지역 미분: \( \frac{\partial y}{\partial z^{2}} \)
활성 함수 전역 미분 : \( \frac{\partial J}{\partial y} \) 와 \( \frac{\partial y}{\partial z^{2}} \)를 곱해서 활성 합수 전역 미분 \( \frac{\partial J}{\partial z^{2}} \)를 계산한다.
가중치 업데이트

은닉 계층에 미분 전달

3. 은닉 계층 미분 전달

Unit의 오차
- Unit의 가중 입력 \( z_{j}^{l} \)이 제곱오차에 미치는 변화율
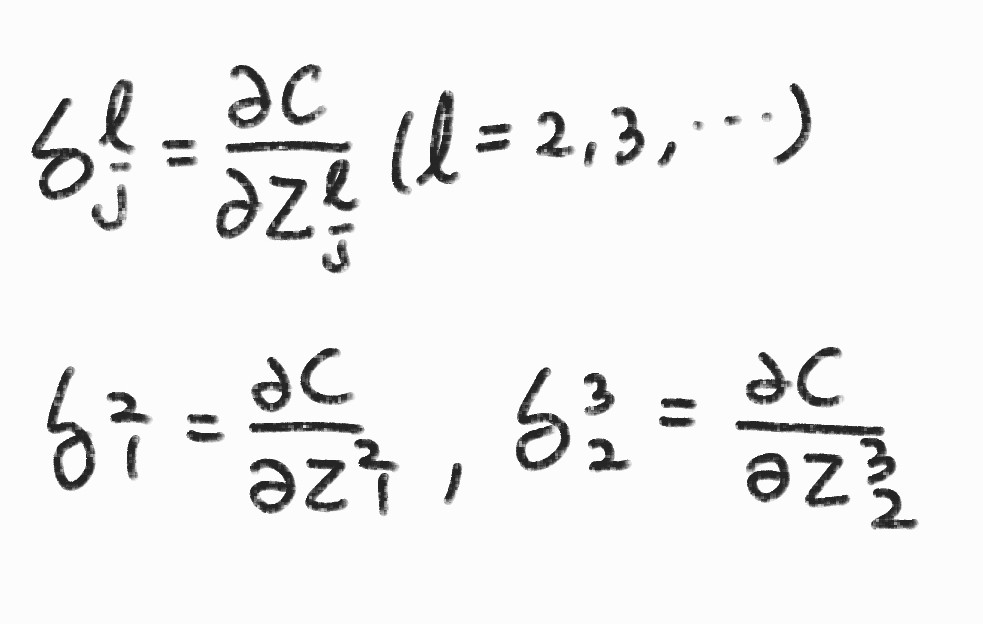

\( \frac{\partial C}{\partial z_{1}^{2}}\frac{\partial z_{1}^{2}}{\partial w_{11}^{2}} \) 을 \( \delta_{j}^{l} \)으로 표현하기

\( \delta_{j}^{l} \) 일반화 하기
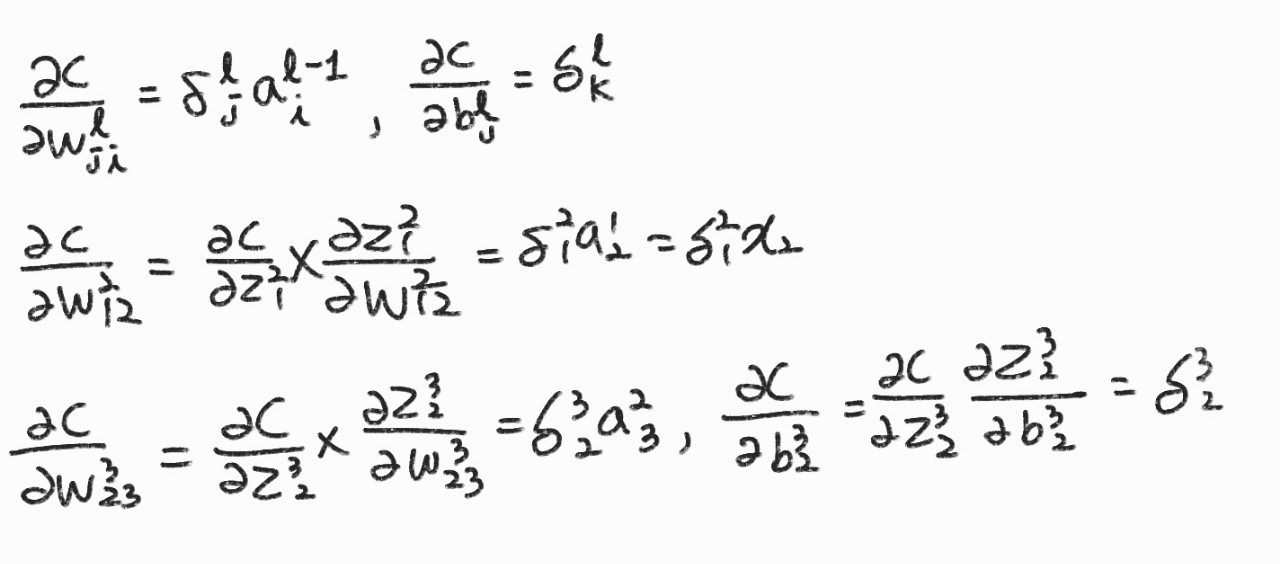
오차역전파
- \( \delta_{j}^{l} \)를 정의하는 방법( \( l \)층 \( j \) 번째)
- Multi layer perceptron을 학습시키기 위한 방법
- Output layer에서의 error의 변화량을 앞선 layer들로 전파하는 방법
- 미분을 통하여 접근함
출력층의 \( \delta_{j}^{l} \) 계산


은닉층 \( \delta_{j}^{l} \) '역' 점화식
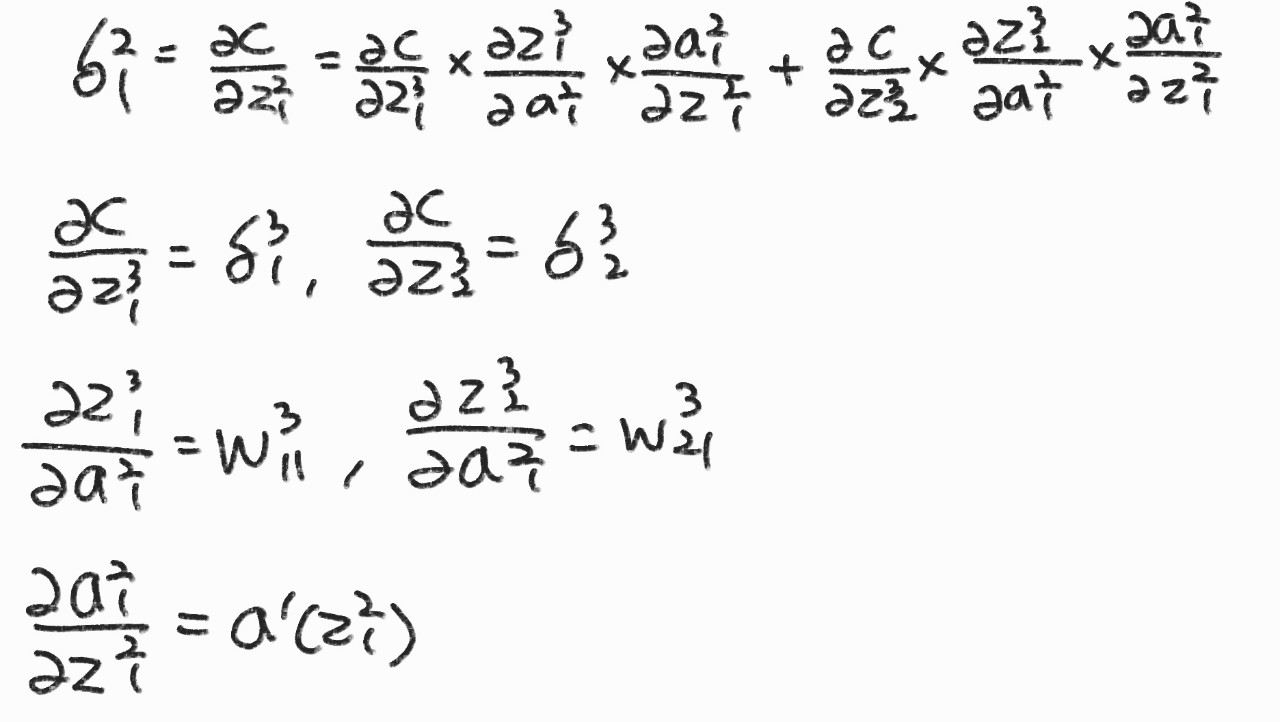

일반화 \( \delta_{j}^{l} \delta_{j}^{l+1} \) 관계
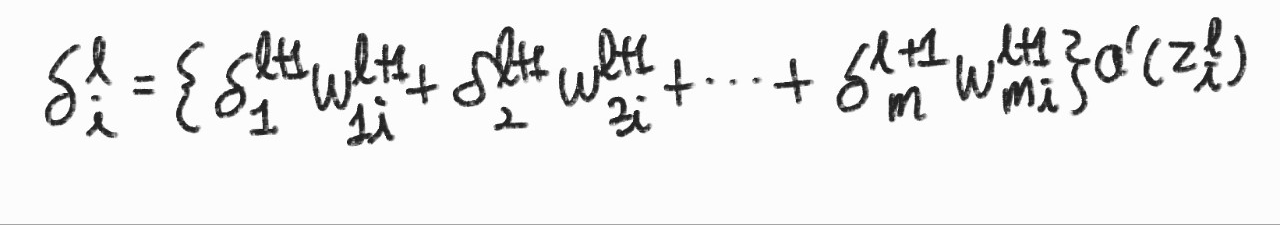
\( w_{11}^{2} \) 갱신

출력층 유닛의 오차만으로 다른 유닛의 오차를 미분없이 구할 수 있음
이것이 오차역전파!
'Machine Learning > 이론' 카테고리의 다른 글
| [ML] Image data (0) | 2022.09.29 |
|---|---|
| [ML] Neural Network (0) | 2022.09.27 |
| [ML] 회귀 분석 (Regression Analysis) (0) | 2022.08.27 |
| [ML] 교차 검증 Cross Validatoin (0) | 2022.08.22 |
| [ML] 규제 Regularization (0) | 2022.08.18 |
