그래프는 기존의 머신러닝, 딥러닝 모델이 잘 처리하지 못하는 non-Euclidean 데이터이며 처리하기 어려운 이유는 기존의 모델들은 상대적으로 단순한 데이터 유형에 특화되어 있기 때문임

이미지, 텍스트, 오디오는 인접한 픽셀, 전후 순서 연결 등이 있으며 상하좌우도 없고 고정된 순서도 없는 복잡한 그래프보다는 단순함 이러한 그래프를 데이터를 처리하기 위해 GNN이 등장
선행지식
Graph
https://pasongsong.tistory.com/237
- Graph란 Vecties(꼭짓점, 정점)와 edges(간선)으로 이루어진 데이터 구조를 말함

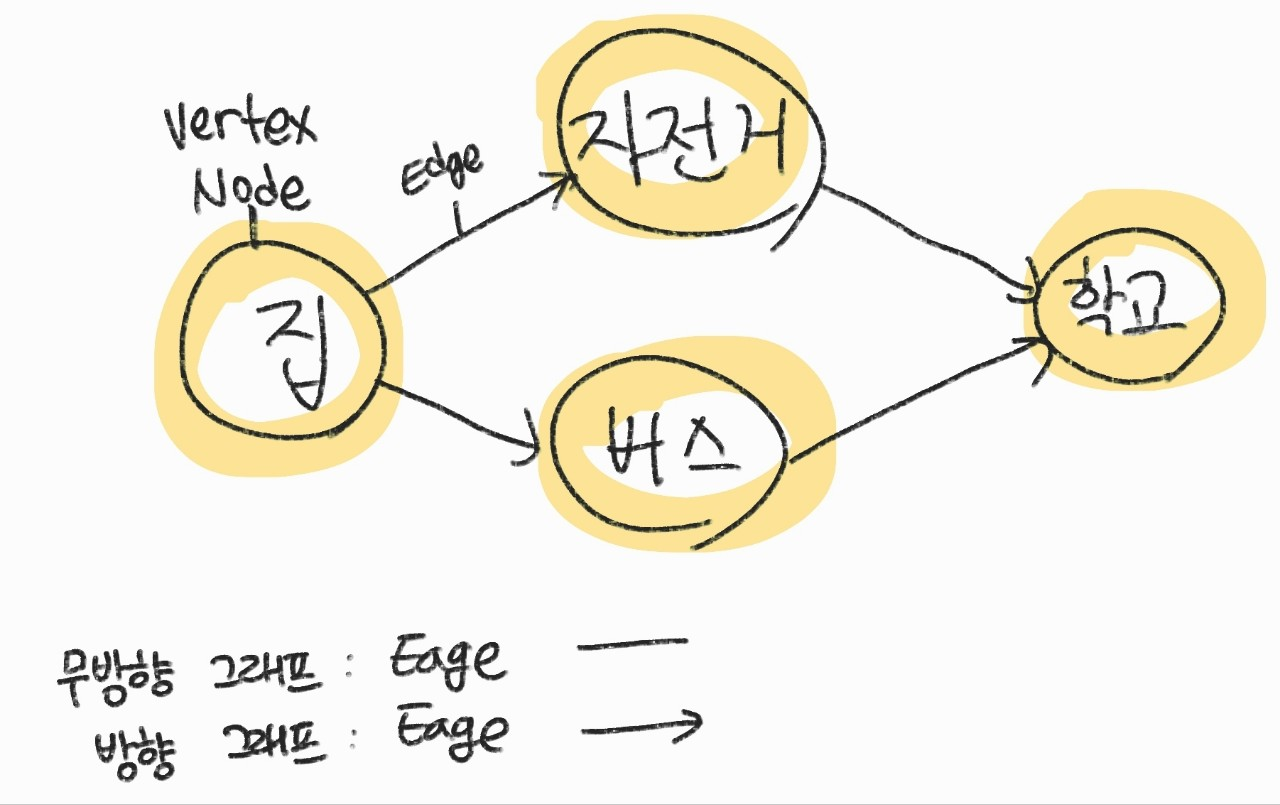
정의는 G=(V, E)로 정의되며 V는 node set, E는 Edge set이다. V는 데이터의 정보를 담고 있으며, E는 데이터 간의 관계 정보가 포함되어 있다.
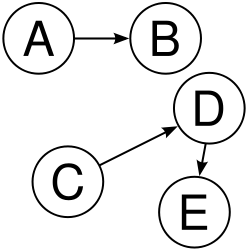
$$ G=(V,E) $$
$$ V = \{A,B,C,D,E\} $$
$$ E = \{(A,B),(C,D),(D,E)\} $$
인접 행렬(Adjacency matrix)로 나타내면 아래와 같다.
n개의 노드가 있다면 크기는 nxn이 되며, 연결 여부(Aji)에 따라 0, 1의 성분을 가진다.
ML에서 그래프를 다룰 때는 점의 특징을 묘사한 feature matrix로 표현하기도 하는데 이는 feature의 개수가 f라면 nxf의 차원을 가
| A | B | C | D | E | |
| A | 0 | 1 | 0 | 0 | 0 |
| B | 0 | 0 | 0 | 0 | 0 |
| C | 0 | 0 | 0 | 1 | 0 |
| D | 0 | 0 | 0 | 0 | 1 |
| E | 0 | 0 | 0 | 0 | 0 |
정점은 한 시스템의 구성요소를 의미하며, 간선은 각 정점들 사이의 관계 또는 상호작용을 표현하는 요소로 볼 수 있다. 그래프는 정점과 간선들로 정의되며, 정점의 위치 정보 또는 간선의 순서 등 그 외의 정보는 일반적으로 그래프의 정의에 포함되지 않는다.
Node Representation(=Node Embedding)
ML에서는 벡터로 표현된 instance를 입력으로 받기 때문에 그래프를 벡터로 표현해야 한다.
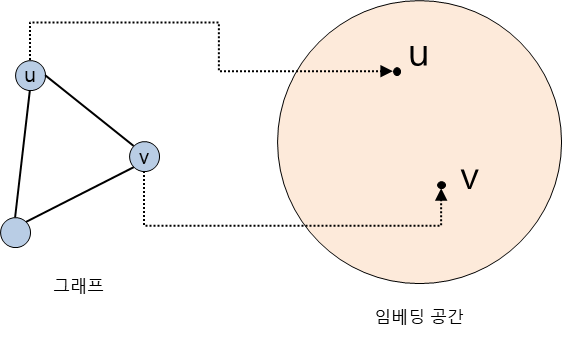
- 그래프의 node(정점)을 벡터로 표현해야 하며, 그 표현 방법을 Node Representation(=node embedding)이라고 함
Node embedding
- node의 vector 표현 그 자체
- node가 표현되는vector space를 embedding Space라고 부름

Network상에서의 유사도가 임베딩에서의 유사도로 잘 나타낼 수 있도록 하는 것으로 임베딩을 하면 많은 종류의 down stream task 수행이 가능해진다.
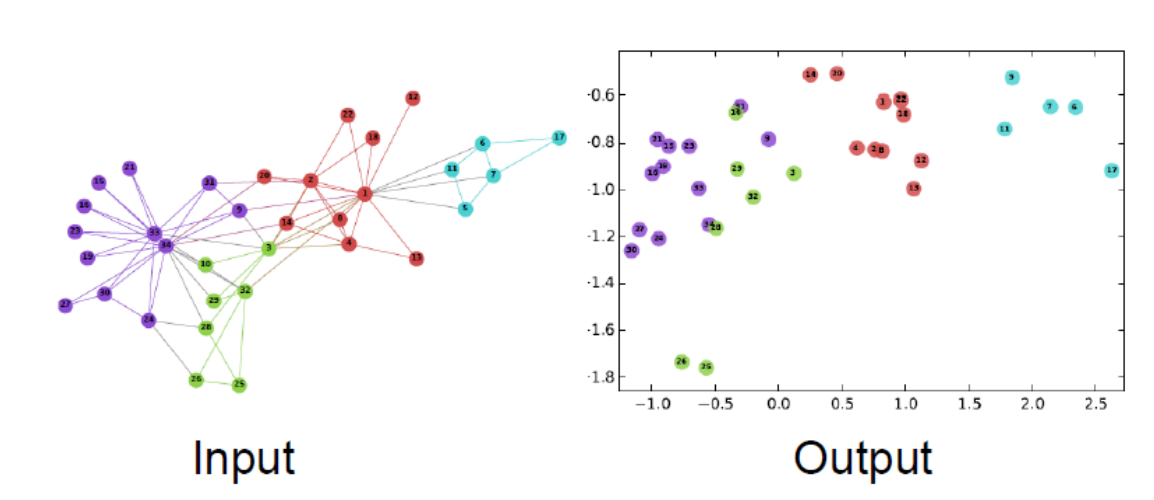
Node embedding 방식은 2가지가 있다.
- 변환식 방법(Transductive method)/ 변환, 전의, 전도, 전환 등 다양하게 쓰이고 있으니 transductive로 기억하는 것이 좋
- 귀납식 방법(Inductive method)
(추후 포스팅 예정)
GNN(Graph Neurel Network)
GNN은 그래프에 직접 적용할 수 있는 신경망으로, 점 선 그래프 레벨에서의 예측 작업에 쓰인다. 유사도는 같으나 Encoder의 구조가 달라진다. cnn, rnn, dnn 등의 딥러닝 방법론들을 차용하여 multiple layers of non-linear transformations based on graph structure를 구성하게 된다.
해결 가능한 문제
GNN으로 예측하게 되는 대상은 노드, 엣지, 그래프 전체가 된다.


- Node classification: Node embedding을 통해 점들을 분류하는 문제
- Link Prediction: 그래프 두 점 사이에 얼마나 연관성이 있는지 예측하는 문제
- Community detection: 밀집되어 연결된 노드의 클러스터들을 식별
- Network similarity: 두개의 sub networks들이 얼마나 비슷한지
Notation
\( V \): vertex set 노드 집합
\( A \): adjacency matrix, 인접행렬
\( v \): \( V \) 의 어떤 한 노드
\( N(v) \): 노드 v의 이웃노드 집합
\( X \in R^{m} \times \mid V \mid \): 노드 변수들
GCN(Graph Convolution Networks)
CNN 방법론을 차용하여 그래프에 접목한 GCN
Propagation
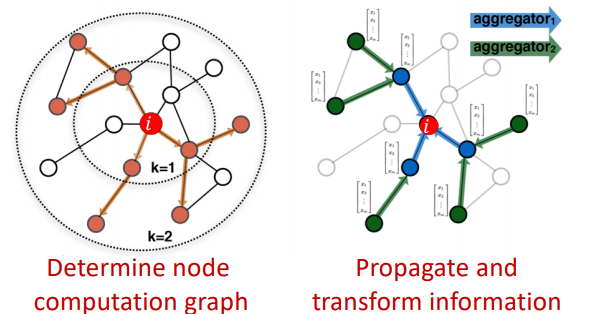
- 2개의 순전파 과정을 거침
- Determine node computation graph
- propagate and transform information
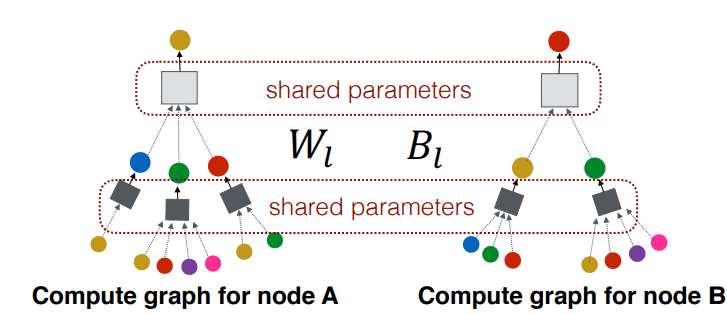
1. 각 노드별 그래프 생성
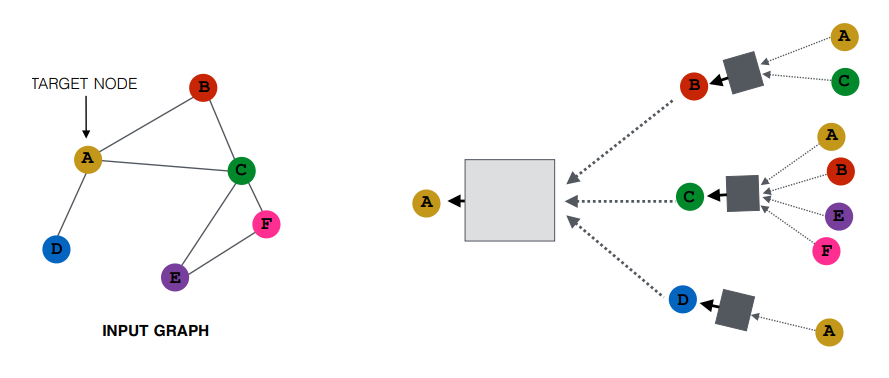
그래프가 준비 된 상황에서 target A node에 대한 계산 그래프 그림이다.
A는 이웃노드 B, C, D로부터 정보를 받으며 B, C, D는 또다시 그 들의 이웃 노드로부터 정보를 받는다.
A, B, C, D, E, F에 대한 계산 그래프는 아래와 같으며 노드마다 각기 다른 형태의 계산 그래프를 가진다. 보라색(E)과 핑크색(F) 같은 경우는 같은 계산 그래프를 가지고 있으며 돌일한 모델을 통해 처리될 수 있음을 뜻한다.


Layer0에서의 노드 정보가 합쳐서(aggreate) 다음 레이어로 전달되고 Layer 1에서의 노드 임베딩 벡터 연산을 거쳐 layer 2로 전달된다.
여기서 동일한 노드라고 해도 Layer0에서의 임베딩 벡터와 Layer 1에서의 임베딩 벡터가 다를 수 있음을 유의해야한다.
2. 순전파, Neighborhood Aggregation
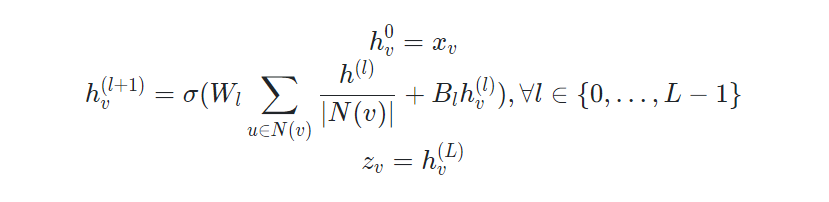
이웃 노드의 정보를 모으는 가장 간단하고 단순한 방법은 평균합이다.
첫 번째 hidden layer는 입력값으로 각 노드의 변수 벡터, 임베딩 벡터를 받는다.
두 번째부터 마지막 hidden layer는 각 layer의 이웃 노드의 벡터의 평균과 이전 layer의 해당 노드(v)를 선형 변환한 것을 결합하여 활성화 함수를 통과함
파라미터는 \( W_{i}, B_{i} \)(이웃노드, 이전노드) 두 행렬이 전부며 즉 모든 계산 그래프는 동일한 가중치는 공유한다.
3. Matrix Formulation
연산을 행렬단위로 진행하여 효율적인 계산이 가능(공부 필요)
학습 과정
비지도 학습

비지도 학습에서의 손실함수는 위와 같으며, 유사도는 랜덤 워크 등의 방법이 사용되고, 디코더는 내적이 사용된다.
지도학습
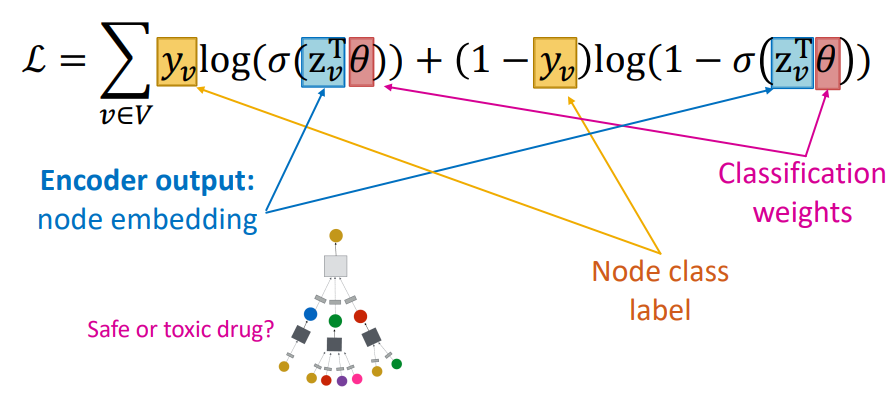
지도 학습에서의 손실함수는 위와 같다. 지도학습은 각 노드의 레이블을 예측하는 방식으로 손실함수를 구한다.
References
- https://pseudolab.github.io/GNN%EC%8A%A4%ED%84%B0%EB%94%94/
- https://didi-universe.tistory.com/entry/GNN-1Graph-Neural-NetGNN-Basic
- https://velog.io/@hmym7308/GNN
- https://glanceyes.com/entry/%EC%B6%94%EC%B2%9C-%EC%8B%9C%EC%8A%A4%ED%85%9C-GNNGraph-Neural-Network%EC%99%80-%EC%9D%B4%EB%A5%BC-%EC%9D%91%EC%9A%A9%ED%95%9C-NGCFNeural-Graph-Collaborative-Filtering%EC%99%80-LightGCN
'NLP' 카테고리의 다른 글
| 프롬프트 엔지니어링 prompt-engineering 기초 (0) | 2024.02.26 |
|---|---|
| NER 기초 (0) | 2024.02.08 |
| Seq2Seq + Attention 코드로 이해하기 (2) | 2023.12.15 |
| [NLP] NLP를 위한 CNN (0) | 2023.05.28 |
| [NLP] LSTM(Long Short-Term Memory) (0) | 2023.05.26 |
