다중 분류 모델
3개 이상의 Class를 분류하는 모델
이는 주사위를 굴렸을 때 각 면이 나올 확률을 예측하는 문제와 같다. 주사위 각 면이 나올 확률 분포는 카테고리 분포로 정의되므로, 다중 분류 모델을 카테고리 분포를 예측하는 모델로 정의할 수 있다.
카테고리 분포
$$ p(x|\mu) = \prod_{k=1}^{K}(\mu_{k})^{x_{k}} $$
$$ \mu = (\mu_{1},\mu_{2},\cdots,\mu_{K})^{T}, \sum_{k=1}^{K}\mu = 1 $$
$$ x = (x_{1},x_{2},\cdots,x_{K})^{T}, x_{k}= 1(k=i), 0(k\neq i), i\in \{1,2,\cdots,K\} $$
- K = 사건 개수
- \( \mu_{k} \) 사건 \( k \)가 발생할 확률
- \( \mu = ( \mu_{1},\mu_{2},\cdots,\mu_{K})^{T} \)은 0과 1로 표현되는 확률 변수
주사위로 예시를 들면
- K = 6
- 숫자 1이 나올 확률 변수 x = (1, 0, 0, 0, 0, 0)
- 숫자 2이 나올 확률 변수 x = (0, 1, 0, 0, 0, 0)
- 숫자 3이 나올 확률 변수 x = (0, 0, 1, 0, 0, 0)
- 숫자 4이 나올 확률 변수 x = (0, 0, 0, 1, 0, 0)
- 숫자 5이 나올 확률 변수 x = (0, 0, 0, 0, 1, 0)
- 숫자 6이 나올 확률 변수 x = (0, 0, 0, 0, 0, 1)
- \( \mu = (\frac{1}{6},\frac{1}{6},\frac{1}{6},\frac{1}{6},\frac{1}{6},\frac{1}{6})^{T} \)
\ ( p(x = (1,0,0,0,0,0)^{T};\mu) = \mu_{1} = \frac{1}{6} \) 숫자 1일 나올 확률로 나머지도 비슷하게 표기할 수 있다.
카테고리 분포의 확률 질량 함수의 그래프는 막대 그래프로 표현한다.
$$ p(t_{i}|x_{i};\theta) = Category(t_{i};\mu(x_{i};\theta)) = \prod_{k=1}^{K}\mu(x_{i};\theta)_{k}^{t_{ik}} $$
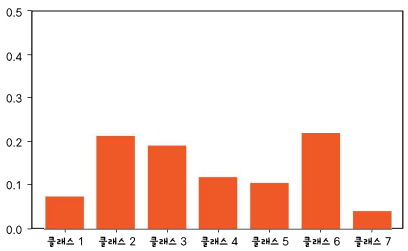
출력 계층의 활성 함수
K개의 클래스중 하나의 클래스에 속할 확률을 구해야하기 때문에 Softmax 함수를 사용한다.
Softmax는 각 클래스에 속할 수치 또는 로짓을 실수 벡터로 출력하고 이를 카테고리 분포의 확률 벡터 \( \mu \)로 변환한다.
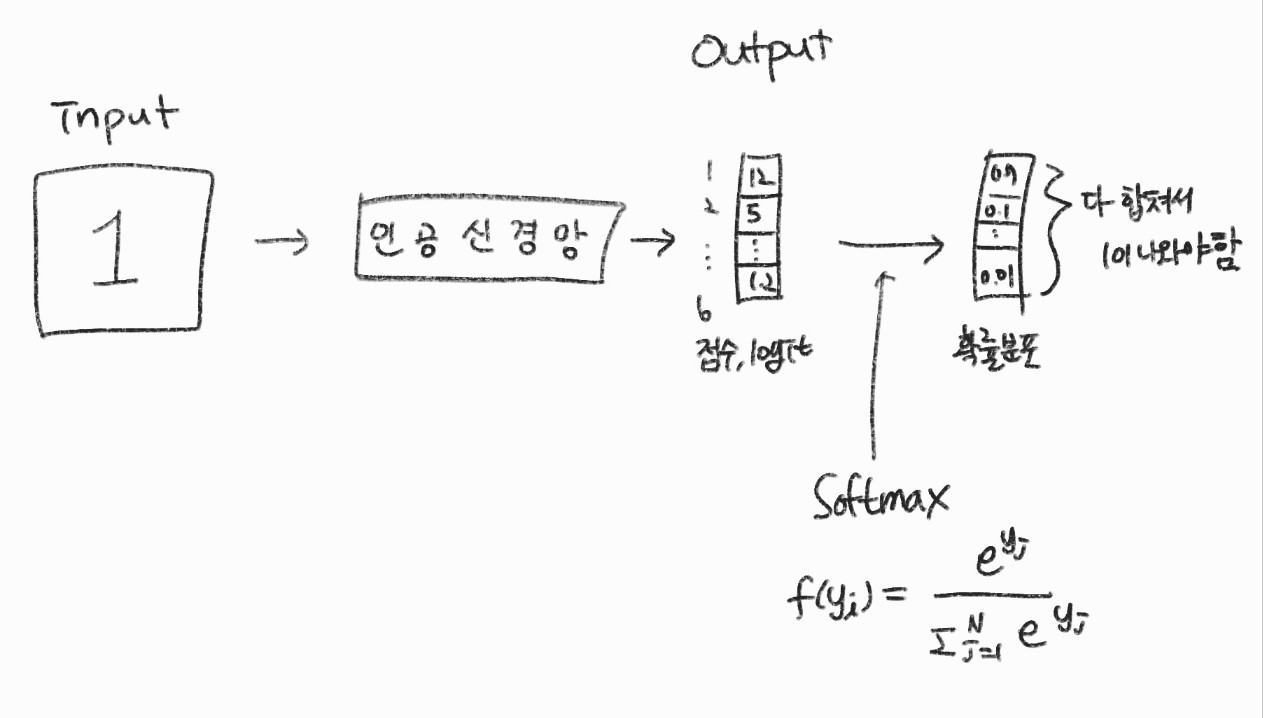
이진 분류 문제도 softmax를 사용할 수 있다.
이진 분류의 신경망 출력은 클래스 1의 발생 확률 하나만 실수값으로 나오고
다중 뷴류의 신경망 출력은 크기가 K인 실수 벡터가 된다.
'Machine Learning > 기법' 카테고리의 다른 글
| [ML] 경사하강법 (0) | 2023.01.09 |
|---|---|
| [ML] 회귀 모델 (0) | 2023.01.04 |
| [ML] 활성화 함수 Activation Function (0) | 2022.09.05 |
| [Optimizer] Adam Adaptive Moment (0) | 2022.08.15 |
| [Optimizer] RMSProp Root Mean Sqaure Propagation (0) | 2022.08.15 |
