728x90
Regression Tree
- Tree 조건에 따라 x가 가질 수 있는 영역을 block으로 나누는 개념
- \(c_{m}\) z축의 값 높이
$$ \hat{p}_{mk} = \sum_{m=1}^Mc_{m}I(x \epsilon R_{m}) $$
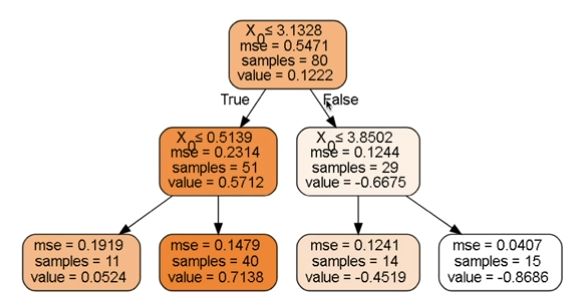
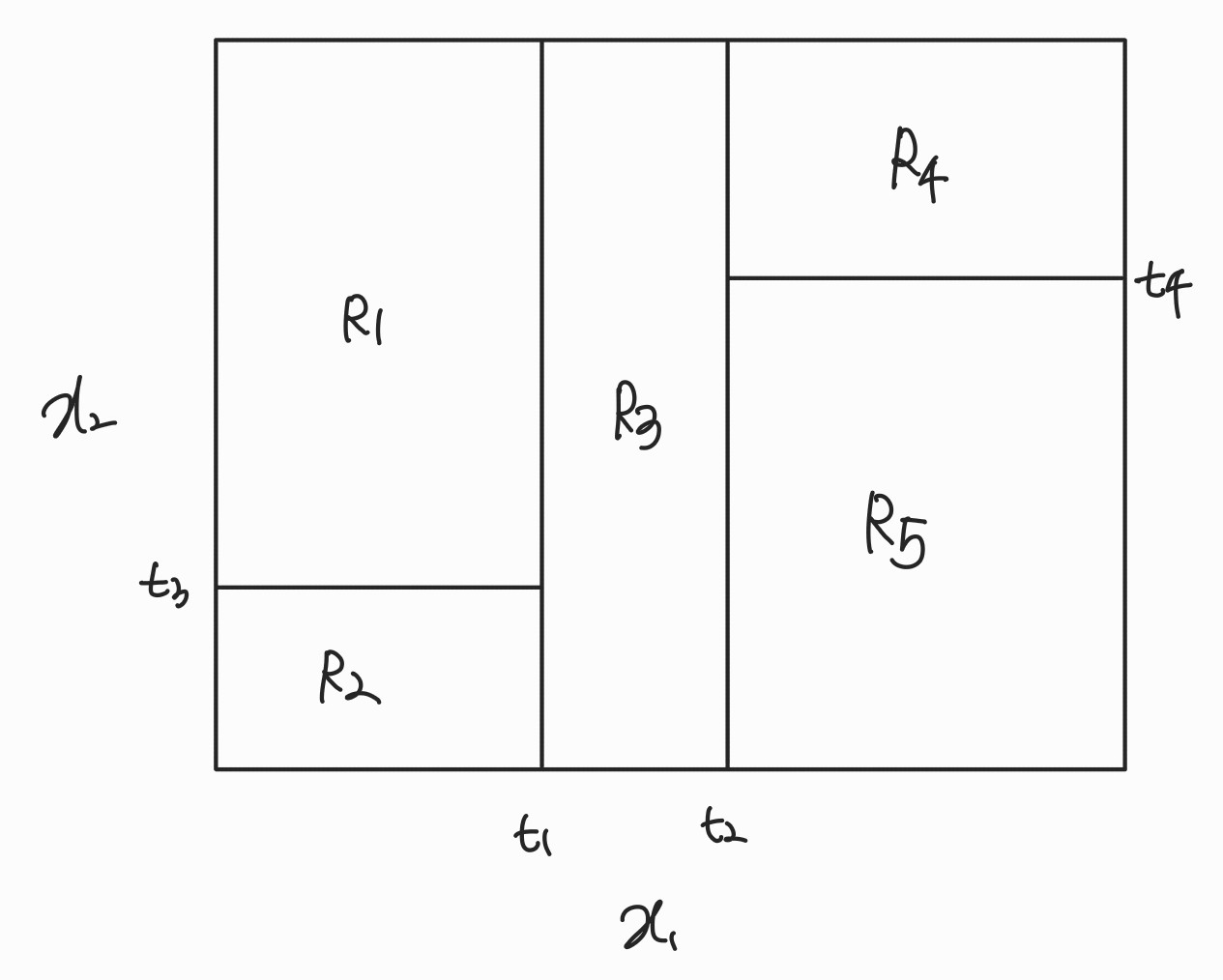
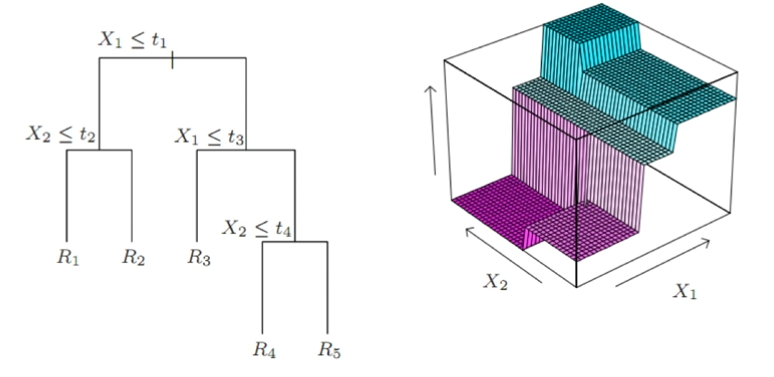
\( R_{m} \) 을 정하는 법
- 임의의 영역을 나눔
- 하나의 실수값을 왼쪽 오른쪽으로 쪼개고 무수히 많은 s를 넣는 것
- \( R_{1}(j,s) = {X|X_{j}<= s} \) and \( R_{2}(j,s) = {X|X_{j}> s} \)
- 각 영역들에 대해, measure를 가장 좋은 값으로 만드는 변수와 기준을 선택함
- 왼쪽 오른쪽 값에 대한 y와 c(평균값)의 차이의 합을 구할 수 있음
- \( min_{j,s}[min_{c1} \sum_{x_{i} \epsilon R_{1}(j,s)} (y_{i}-c_{1})^{2} +min_{c2} \sum_{x_{i} \epsilon R_{2}(j,s)} (y_{i}-c_{2})^{2} ] \)
Y구하기
- \( \hat{c}_{m} = avg(y_{i}|x_{i} \epsilon R_{m}) \)
- \( \hat{y} = \hat{f}(x) = \sum_{m=1}^M I(x \epsilon R_{m}) \)
728x90
'Machine Learning > Model' 카테고리의 다른 글
| [ML] DBSCAN clustering Density-based spatial clustering of applicatoins with noise (0) | 2022.09.06 |
|---|---|
| [ML] Hierarchical clustering (0) | 2022.09.06 |
| [ML] K-means clustering (0) | 2022.09.06 |
| [ML] 분류 트리 Classification Tree (0) | 2022.08.29 |
| [ML] 의사결정나무 Decision Tree (0) | 2022.08.29 |
728x90
Regression Tree
- Tree 조건에 따라 x가 가질 수 있는 영역을 block으로 나누는 개념
- cmcm z축의 값 높이
ˆpmk=M∑m=1cmI(xϵRm)^pmk=M∑m=1cmI(xϵRm)



RmRm 을 정하는 법
- 임의의 영역을 나눔
- 하나의 실수값을 왼쪽 오른쪽으로 쪼개고 무수히 많은 s를 넣는 것
- R1(j,s)=X|Xj<=sR1(j,s)=X|Xj<=s and R2(j,s)=X|Xj>sR2(j,s)=X|Xj>s
- 각 영역들에 대해, measure를 가장 좋은 값으로 만드는 변수와 기준을 선택함
- 왼쪽 오른쪽 값에 대한 y와 c(평균값)의 차이의 합을 구할 수 있음
- minj,s[minc1∑xiϵR1(j,s)(yi−c1)2+minc2∑xiϵR2(j,s)(yi−c2)2]minj,s[minc1∑xiϵR1(j,s)(yi−c1)2+minc2∑xiϵR2(j,s)(yi−c2)2]
Y구하기
- ˆcm=avg(yi|xiϵRm)^cm=avg(yi|xiϵRm)
- ˆy=ˆf(x)=∑Mm=1I(xϵRm)^y=^f(x)=∑Mm=1I(xϵRm)
728x90
'Machine Learning > Model' 카테고리의 다른 글
| [ML] DBSCAN clustering Density-based spatial clustering of applicatoins with noise (0) | 2022.09.06 |
|---|---|
| [ML] Hierarchical clustering (0) | 2022.09.06 |
| [ML] K-means clustering (0) | 2022.09.06 |
| [ML] 분류 트리 Classification Tree (0) | 2022.08.29 |
| [ML] 의사결정나무 Decision Tree (0) | 2022.08.29 |
