[ML] 분류 트리 Classification Tree

Classification Tree

• Tree 조건에 따라 x가 가질 수 있는 영역을 block으로 나누는 개념

$$ \hat{p}_{mk} =   \frac{1}{N_{m}}  \sum{x_{i} \epsilon R_{m}I(y_{i}=k)}   $$

상대 비율

classification tree를 2차원으로 나타낸 것

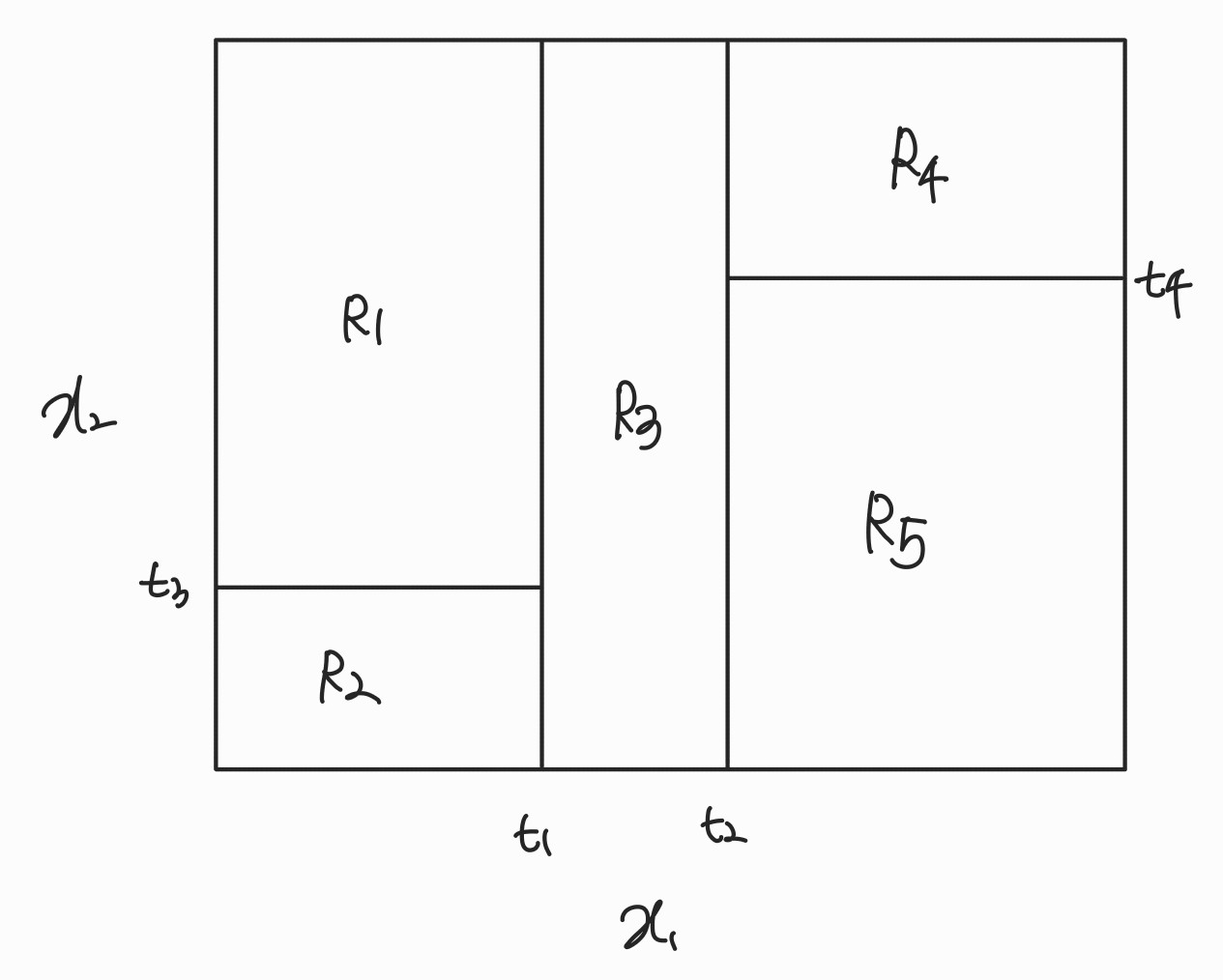
\( R_{m} \)을 정하는 법

• 범주형 : 범주에 따라 구성
• 연속형 : 영역을 임의로 나누고 영역에 따라 구성

구성된 영역에 대해 measure를 가장 좋은 값으로 만드는 변수와 기준을 선택함

영역 나눌 때 사용되는 도구

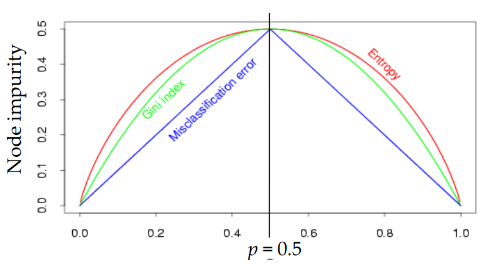
• 아래의 값이 작아지도록 R을 나눔
• 엔트로피
•  오분류율
  • R안의 샘플 중 실제값과 예측값이 다른 경우의 개수를 셈
  • \( \frac{1}{N_{m}} \sum_{i \epsilon R_{m}} I(y_{i} != k(m)) = 1- \hat{p}_{mk(m)} \)
• Gini index
  • \( \sum_{k!= \acute{k}}  \hat{p}_{mk} \hat{p}_{m \acute{k}} =  \sum_{k=1}^K  \hat{p}_{mk}(1- \hat{p}_{mk}) \)

---

Y범주 추정하기

• \( \hat{p}_{mk} \) 가 커지는 k를 정함
• \( \hat{p}_{mk} =  \frac{1}{N_{m}} \sum_{x_{i} \epsilon R_{m}} I(y_{i}=k)  \)
• \( k_{m} = argmax \hat{p}_{mk}  \)

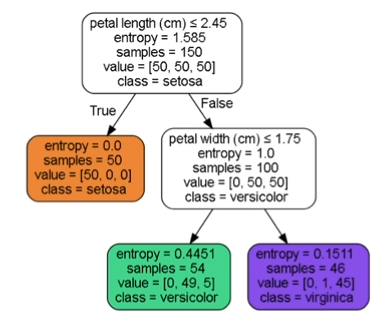
\( \hat{p}_{msetosa} = 1  \)

\( \hat{p}_{mversicolor} = \frac{49}{54} \)

\( \hat{p}_{mvirginica} = \frac{45}{46} \)