Machine Learning/이론
배깅 Bagging
파송송
2023. 11. 14. 16:38
728x90
Ensemble
https://pasongsong.tistory.com/317
앙상블은 조화 또는 통일을 의미하며 어떤 데이터의 값을 예측한다고 할 때, 하나의 모델이 아닌 여러 개의 모델을 조화롭게 학습시켜 모델의 예측 결과를 이용하여 강건한 예측값을 구하는 것이다.
크게 Ensemble의 기법으로 배깅(Bagging)과 부스팅(Boosting)이 있다.
배깅(Bagging)
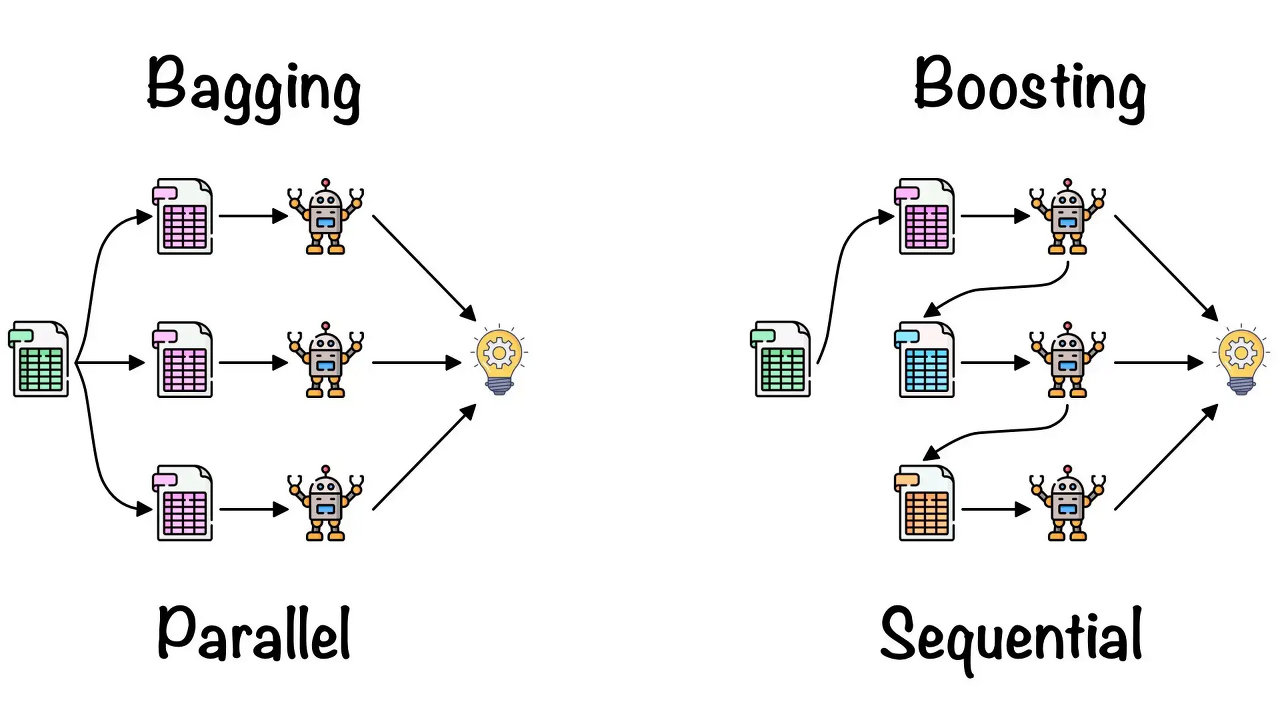
- 모델을 쌓아서 각 예측값을 합산하여 최종 예측값을 예측한다.
- Input : 각 Ensemble 모델의 예측값
- Target : 합산한 최종 예측값

- Bootstrapp Aggregating의 약자로 Ensemble의 각 모델이 서로 다른 데이터셋을 이용하여 예측값을 내고 이를 종합하여 최종 예측값을 결정한다.
- 각 데이터셋은 복원 추출(sampling with replacement)을 통해 원래 데이터의 수만큼의 크기를 갖도록 샘플링한다.
- 개별 데이터셋을 Bootstrap이라고 부른다.
- Bootstrap은 각 데이터가 동등한 확률로 샘플링 되고 겹치는 데이터로 인해 분포 왜곡을 시키며 각 Bootstrap이 서로 다른 noise를 갖는 효과를 준다. > Variance 낮춤
한 데이터(개체)의 확률
- OOB(Out Of Bag): 하나의 Bootstrap에 한 번도 선택되지 않은 데이터
- 위와 같이 샘플링이 된다면 한 데이터가 하나의 Bootstrap에 한 번도 선택되지 않은 경우가 생긴다. 이때의 확률은 아래와 같다
- \( p=\left ( 1-\frac{1}{N} \right )^{N} \to lim_{N\to \infty}\left ( 1 - \frac{1}{N} \right ) =e^{-1} = 0.368 \)
- OOB는 36%확률로 발생한다.

- OOB의 경우 Validation dataset으로 재활용하여 학습한다.
적합한 모델
- 이는 Variance가 높고 Bias가 낮은 알고리즘에 적합하며 이는 Bootstrap을 통해 Variance를 낮출 수 있기 때문이다.
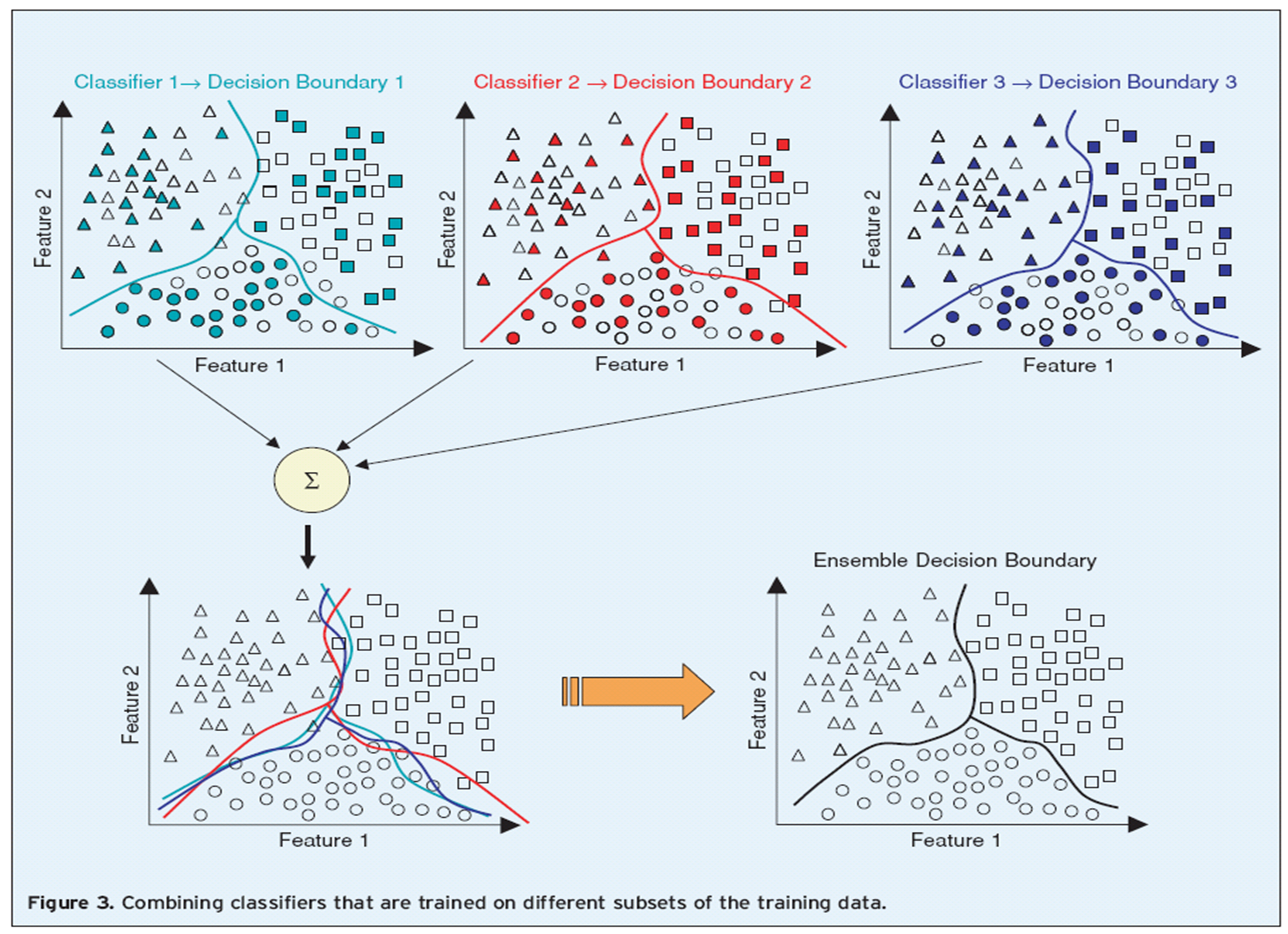
- 투명한 데이터는 한번도 선택되지 못한 OOB이고 색이 있는 도형은 한 번 이상 선택된 데이터이다.
- 중복 데이터를 통해 각 Bootstrap이 다양한 Variance로 추론(다양성 확보)하고 이를 합산하여 최종 결괏값을 내기 때문에 Variance가 낮아지는 것이다.
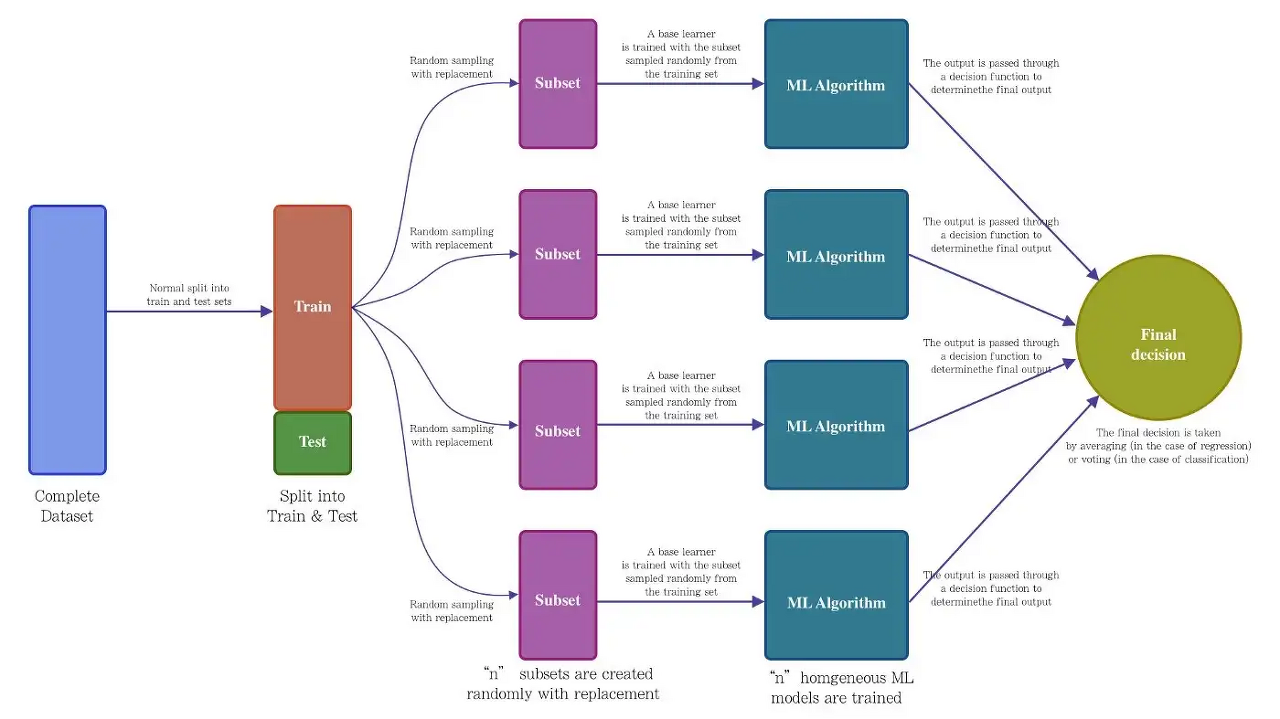
- Bagging의 Process를 보면 ML Algorithm이 있고 여기에는 Decision Tree, MLP, KNN 등 다양한 모델을 넣을 수 있다.
- 하지만 Bagging에 효과적인 모델을 쓰는 것이 성능 향상에 좋다.
Aggregation 방법
- Aggregation방법에는 크게 2가지 방법이 있다.
- Majority voting
- Weighted voting
- Training Accuracy에 따른 Weighted voting
- Test instance에 따른 Weighted voting
Majority Voting
| Training Accuracy | Ensemble population | P(y=1) for test instance | predicted class label |
| 0.65 | Model 1 | 0.84 | 1 |
| 0.91 | Model 2 | 0.34 | 0 |
| 0.88 | Model 3 | 0.98 | 1 |
$$ \hat{y}Ensemble = arg \ max_{i}\left ( \sum_{j=1}^{n} \delta (\hat{y}_{j}=j), i\in \left\{ 0,1 \right\} \right ) $$
- 다수결에 의한 추론으로 Predicted class label로 정해진다.
- \( \sum_{j=1}^{n} \delta \left ( \hat{y}_{j}=0 \right ) = 1 \)
- \( \sum_{j=1}^{n} \delta \left ( \hat{y}_{j}=1 \right ) = 2 \)
- \( \hat{y}Ensembel = 1 \)
Weighted voting
$$ \hat{y}Ensemble = arg \ max_{i}\left ( \frac{\sum_{j=1}^{n}\left ( TrnAcc_{j}\cdot \delta \left ( \hat{y}_{j}=i \right ) \right )}{\sum_{j=1}^{n}\left ( TrnAcc_{j} \right )}, i\in \left\{ 0,1 \right\} \right ) $$
- Training Accuracy에 의한 가중치가 포함된다.
- \( \frac{\sum_{j=1}^{n}\left ( TrnAcc_{j}\cdot \delta \left ( \hat{y}_{j}=0 \right ) \right )}{\sum_{j=1}^{n}\left ( TrnAcc_{j} \right )} =0.373 \)
- \( \frac{\sum_{j=1}^{n}\left ( TrnAcc_{j}\cdot \delta \left ( \hat{y}_{j}=1 \right ) \right )}{\sum_{j=1}^{n}\left ( TrnAcc_{j} \right )} = 0.627 \)
- \( \hat{y}Ensembel = 1 \)
$$ \hat{y}Ensemble = arg \ max_{i} \left ( \frac{1}{n} \sum_{j=1}^{n}P\left ( y=i \right ), i\in \left\{ 0,1 \right\} \right ) $$
- test instance에 의한 가중치가 포함된다.
- \( \sum_{j=1}^{n}P\left ( y=0 \right )=0.28 \)
- \( \sum_{j=1}^{n}P\left ( y=1 \right )= 0.72 \)
- \( \hat{y}Ensembel = 1 \)
728x90