Machine Learning/Model
[ML] KNN(K-Nearest Neighborhood), k-최근접 이웃
파송송
2023. 3. 22. 18:41
728x90
KNN(K-Nearest Neighborhood)
- 직관적인 머신러닝 분류(Classification) 알고리즘으로 새로 들어온 관측치 주변의 k개의 sample을 이용하여 관측치를 분류한다.
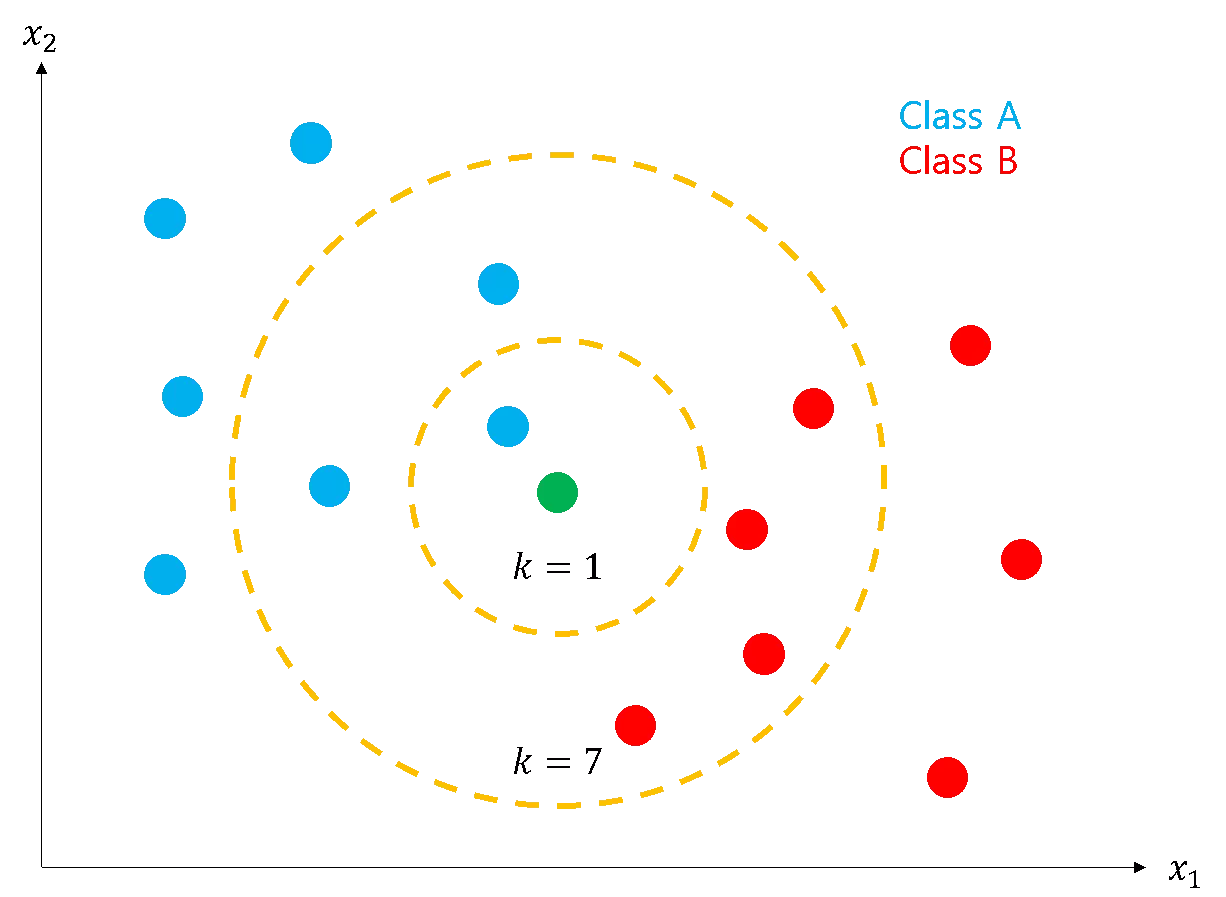
- 아래의 녹색점이 새로 들어온 관측치이다.
- k = 1일 때, 녹색점은 가장 가까운 k개의 데이터 중 파란색이 많기 때문에 Class A로 분류된다.
- k = 7일 때, 녹색점은 가장 가까운 k개의 데이터 중 빨간색이 많기 때문에 Class B로 분류된다.
K 정하기
k는 KNN에서 중요한 파라미터로 너무 작으면 과적합이 발생하고 너무 크면 과소적합이 발생한다.
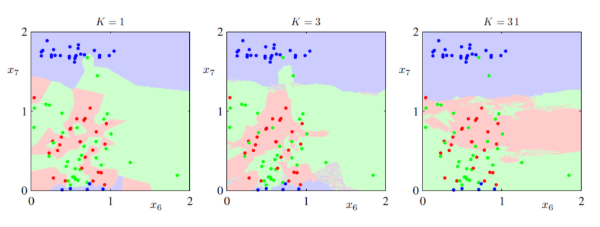
큰 K
- 미세한 경계 부분을 잘 분류하지 못함
- 과소적합이 발생함(모델이 간단해짐)
작은 K
- 이상치의 영향을 크게 받음
- 패턴이 직관적이지 않을 수 있음
- 과적합이 발생함(모델이 복잡해짐)
Majority voting
- 거리에 반비례하는 Weight를 주어 가까운 데이터를 더 중요하게 생각하는 기법
변수에 따른 KNN 방법
범주형 변수
- K-NN 중 가장 많이 나타난 범주를 y로 추정함
- tie문제를 막기 위해 K는 홀수로 지정함(k=2일 때, A=2, B=2 일 때 추정하기 곤란함)
거리
- Hamming distance = \( D_{H} \) = \( \sum_{j=1}^J I(x_{j} \neq y_{j}) \)
- 2개의 변수를 비교하여 다를 때 1 카운트함
- '11011', '10111' 두 값 사이의 Hamming distance는 2 임
연속형 변수
- 일반적으로 K-NN의 대푯값(평균)으로 y를 추정함
- Inverse distance weighted average를 고려할 수 있음(가중 평균)
거리
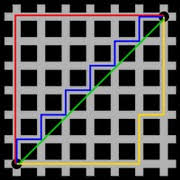
- Euclidian distance
- x와 y의 직선거리
- \( \sqrt{ \sum_{j=1}^J (x_{j}-y_{j})^{2} } \)
- 위의 사진에서 초록선이 유클리디안 거리
- manhattan distance
- x에서 y로 좌표축 발향만으로 이동하여 계산되는 거리
- \( \sum_{j=1}^J |x_{j}-y_{j}|^{2} \)
- 위 사진에서 빨간 선, 파란 선, 노란선이 맨해튼 거리
새로운 관측치 추정
- 새로운 관측치 \( (x, y) \)와 N개의 Training 데이터 \( (X_{i}, Y_{i} \), \(i=1,\cdots,N \)의 관계
- \( (X_{1},Y_{1}),\cdots,(X_{n},Y_{n}) \)
- 새로운 관측치가 들어오면 N개의 데이터들은 새로운 관측치와 거리가 가까운 순서로 정렬됨
- \( d(X_{1}, x) \leq \cdots \leq d(X_{n},x) \)
범주형 종속 변수
- 근처 k개 중에 가장 많은 범주를 선택함
- \( \hat{p}_{m}= \frac{ \sum_{i=1}^k (Y_{i}=m) }{k} , (m=1,\cdots,M) \)
- \( d(X_{1}, x) \leq \cdots \leq d(X_{n},x) \) 에서 각 범주의 확률값을 구함
- \( \hat{y}=argmax_{(m=1,\cdots,M)}\hat{p}_{m} \)
- 가장 확률이 높은 범주가 새로운 관측치의 범주가 됨
연속형 종속 변수
- 근처 k개의 평균을 예측값으로 사용함
- \( \hat{y}= \frac{ \sum_{i=1}^k Y_{{i}} }{k} \) 표본 평균
- inverse distance weighted average를 고려한 평균식
- \( \hat{y}= \frac{ \sum_{i=1}^k \frac{1}{d(x_{i}, x)}\cdot Y_{i}}{k} \)
- 거리 정보를 weight로 추가함
차원의 저주
데이터셋의 차원이 증가할수록 모델의 성능이 저하되는 현상
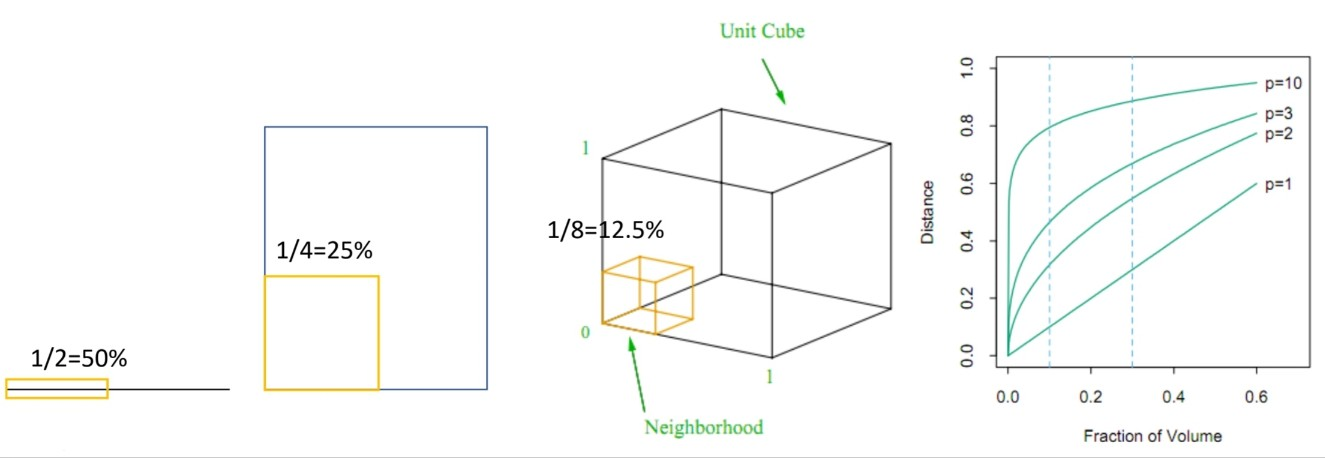
- 각 변수의 50% 영역에 해당하는 자료를 가지고 있을 때, 차원이 커지면 기존에 가지고 있던 데이터로 모집단을 설명할 수 있는 영역이 줄어듦
KNN 차원의 저주
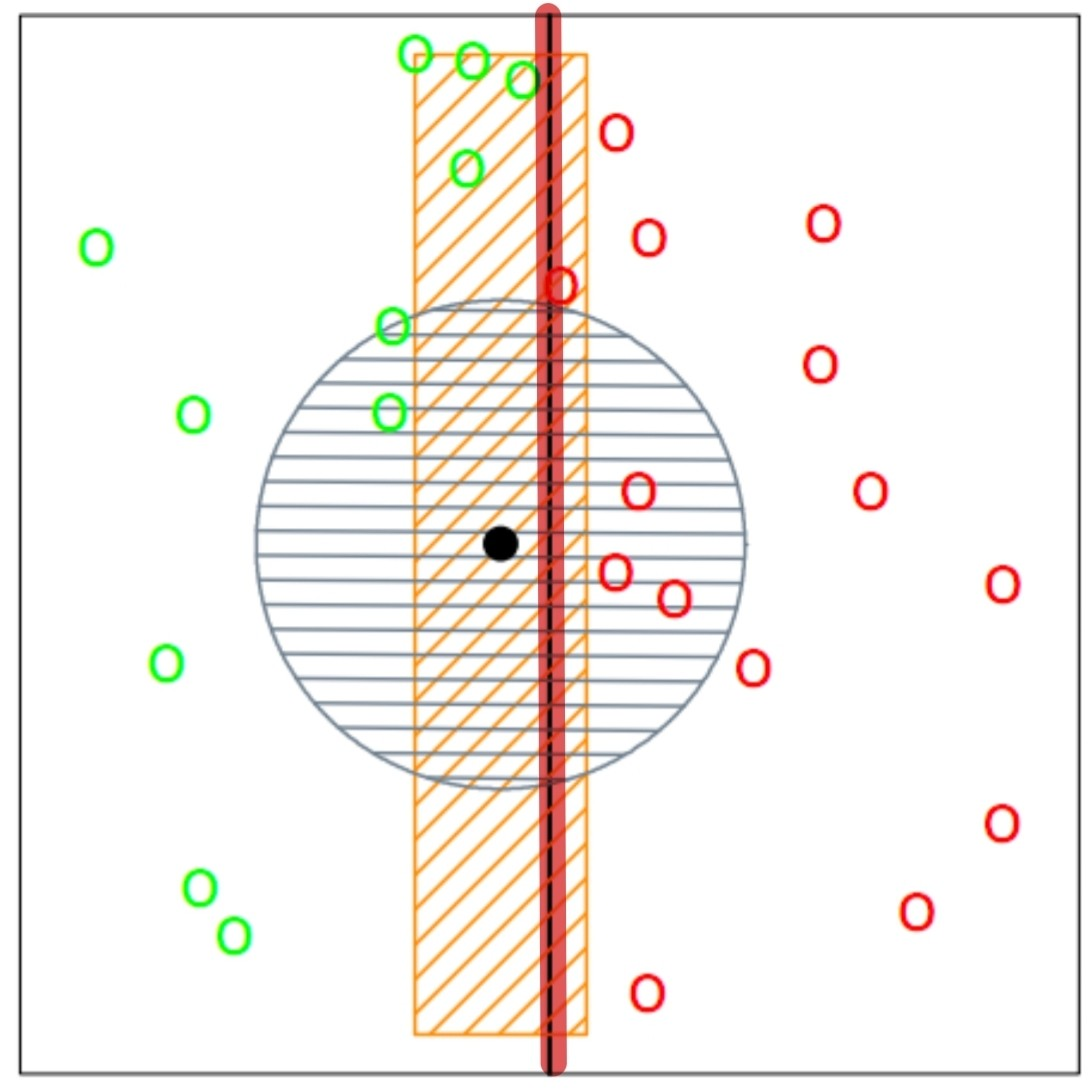
- 직관에 의하면 검은 점은 빨간 선을 기준으로 녹색으로 분류가 돼야 함
- 하지만 녹색과 붉은색의 분류에 영향을 끼치지 않는 필요 없는 변수 y가 있기 때문에 이는 붉은색으로 분류됨
이를 해결하기 위해서 의미 있는 변수를 선별하거나 PCA를 진행한다.
728x90