ELBO

ELBO는 VAE의 loss에도 쓰이는 것으로 variational lower bound라고도 불린다.
ELBO는 \( p(z \mid x) \) 가 다루기 힘든 분포를 이루고 있을 때 이를 다루기 쉬운 분포인 \( q(x) \)로 표현하는 과정에서 두 분포의 차이(KL Divergence)를 최소화하기 위해 사용된다.
수식
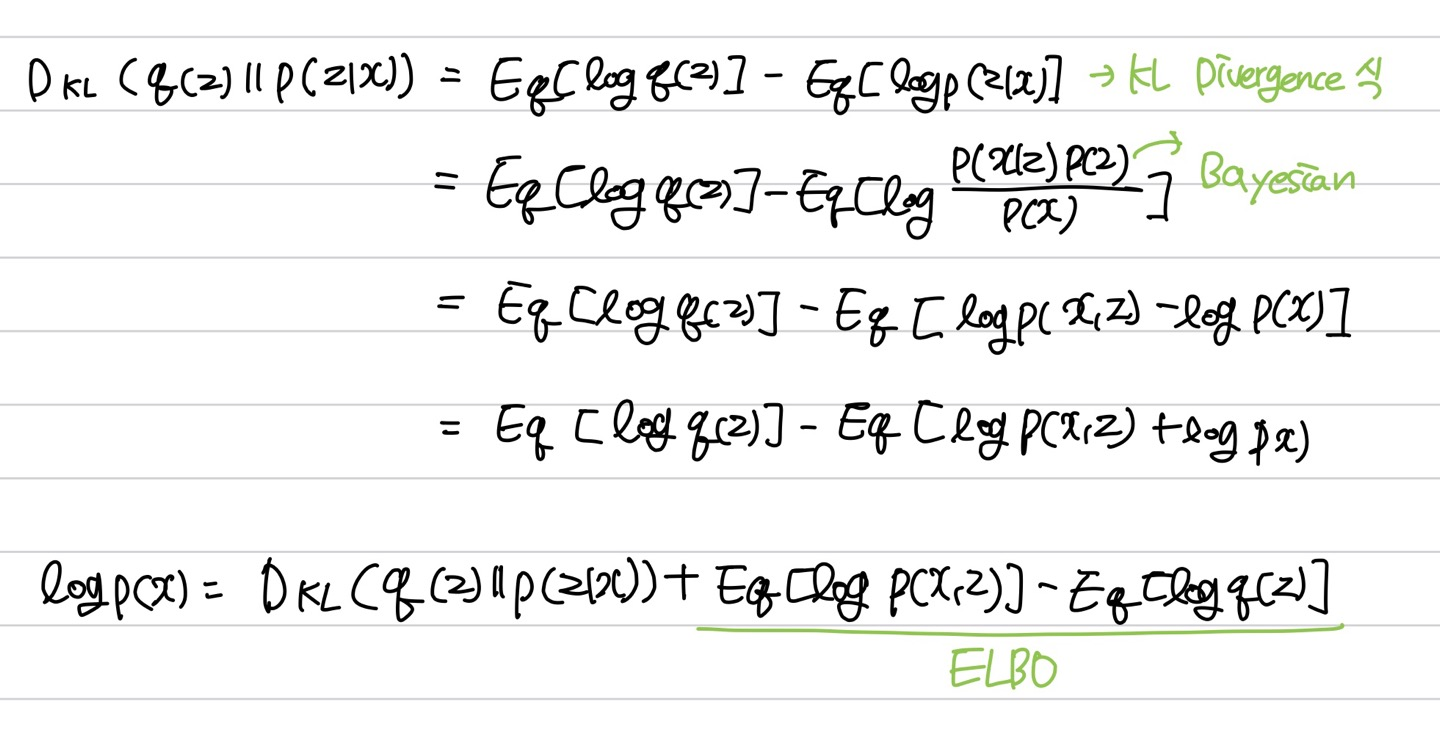
\( log_{\theta} P(x) \)는 모델의 파라미터(\( \theta \))가 주어졌을 때 x가 나올 확률이고 이 확률이 높을 수록 좋은 모델이다. 우리는 \( log_{\theta} P(x) \)를 최대화 하는 방향으로 \( \theta \)를 학습시켜야 한다.
위의 식에서 KL Divergence는 늘 0보다 크거나 같기 때문에 \( log P(x) \)는 ELBO보다 크거나 같고 그렇기에 Lower bound라고 불린다. Evidence lower bound인 이유는 Bayes'Rule에서 \( P(x) \)를 evidence라고 부르기 때문이다.
해석
\( p(x) \)는 costant로 변하지 않을 때 ELBO가 증가하면 \( D_{KL} \)를 감소하기 때문에 ELBO를 최대화하여 \( D_{KL} \)를 최소화시킨다.
ELBO = \( E_{q}[log p(x,z)-E_{q}logq(x)] \)

첫 번째 \( E_{q}[log p(x,z) \) 는 \( \int q(x)logp(x,z) \)로 표현할 수 있고 이는 ELBO를 최대화 시키면 \( q(x) \)기준에서 \( p(x,z) \)가 클 때 \( q(x) \)도 커진다는 뜻이다. 이는 높은 probability가 할당되는 곳에 \( q(x) \)도 할당된다는 뜻이다.
두 번째 \( -E_{q}[log q(z)] \)는 \( q \)의 entropy로 이 값이 증가되면 probabiloty가 골고루 퍼진다.
https://seongukzz.tistory.com/3
https://yonghyuc.wordpress.com/2019/09/26/elbo-evidence-of-lower-bound/
'Machine Learning > 이론' 카테고리의 다른 글
| f1-score 매개변수 average의 종류 (0) | 2024.06.17 |
|---|---|
| 배깅 Bagging (0) | 2023.11.14 |
| [통계] 엔트로피 Entropy, 크로스 엔트로피 Cross Entropy, KL divergence (0) | 2023.06.14 |
| [ML] 인공지능 기초, 개요 (0) | 2023.04.12 |
| [미분] 미분 기초와 모델 학습에 쓰이는 미분 (1) | 2023.03.20 |
