프로그래머스
코드 중심의 개발자 채용. 스택 기반의 포지션 매칭. 프로그래머스의 개발자 맞춤형 프로필을 등록하고, 나와 기술 궁합이 잘 맞는 기업들을 매칭 받으세요.
programmers.co.kr
나의 풀이
n별 타일 개수 구하기
2xn 타일링과 결이 비슷한 문제로 dp를 활용하여 문제를 해결했다.
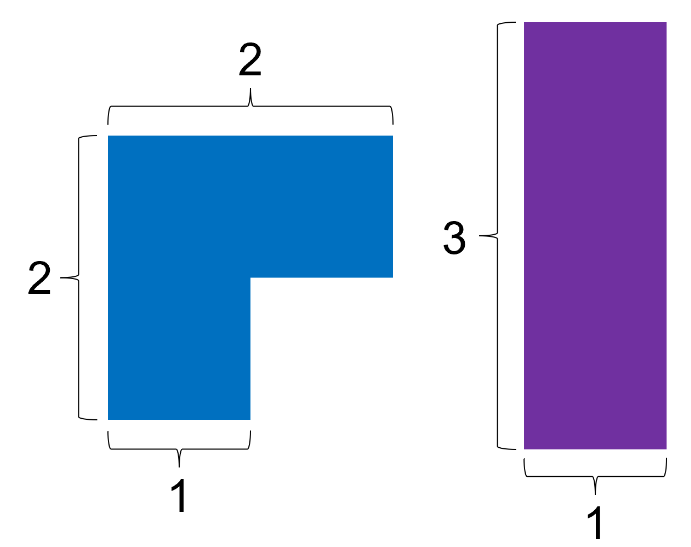
nx3 (n <=3), 의 타일이 있고 그중 일부만 가져오면 아래의 모습과 같다.
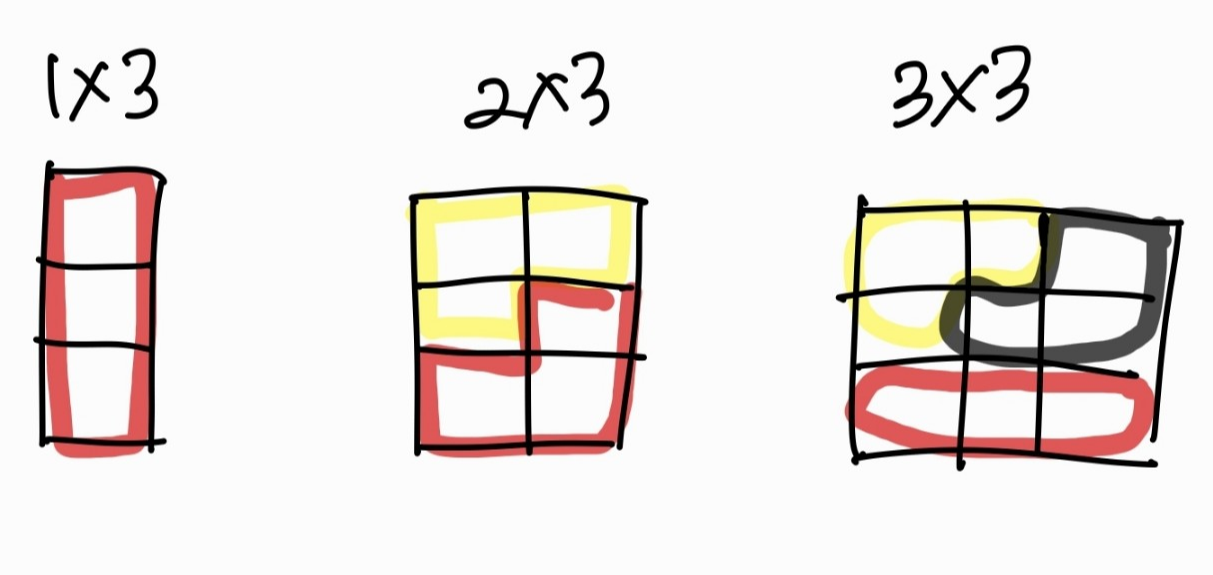
1x3 타일을 1로 2x3 타일을 2로 3x3 타일을 3으로 표현하면,
3x3의 면적을 채우는 타일의 경우의 수는 아래와 같은 방식으로 구할 수 있다.
3x3
(1, 1, 1) -> 1
(1, 2), (2, 1) -> 2x2
(3) -> 5
타일의 개수 = 10
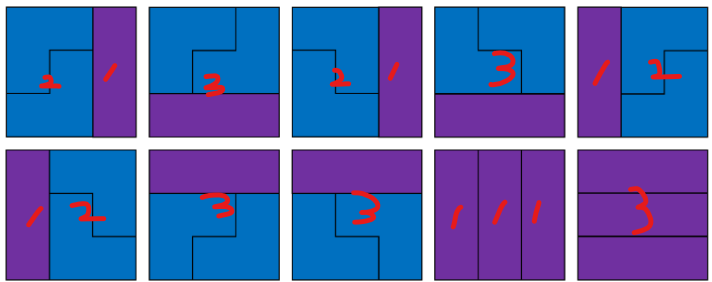
2x3 타일은 경우의 수가 2가 나오기 때문에 2를 곱해준다.
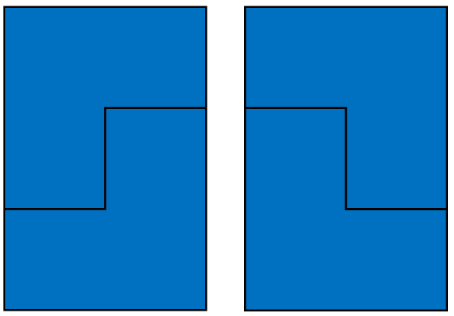
3x3타일은 경우의 수가 5개 나오기 때문에 5를 곱해준다.

규칙 찾기
위의 규칙만 따지면 \( f(x) = f(x-1) + 2\times f(x-2) + 5 \times f(x-3) \)해주면 되지만 고려해야 하는 것이 하나 더 있다.
n이 커짐에 따라 규칙이 늘어난다는 것이고 아래의 규칙을 가진다.
4x3 (4) -> 2
5x3 (5) -> 2
6x3 (6) -> 4
7x3 (7) -> 2
8x3 (8) -> 2
9x3 (9) -> 4
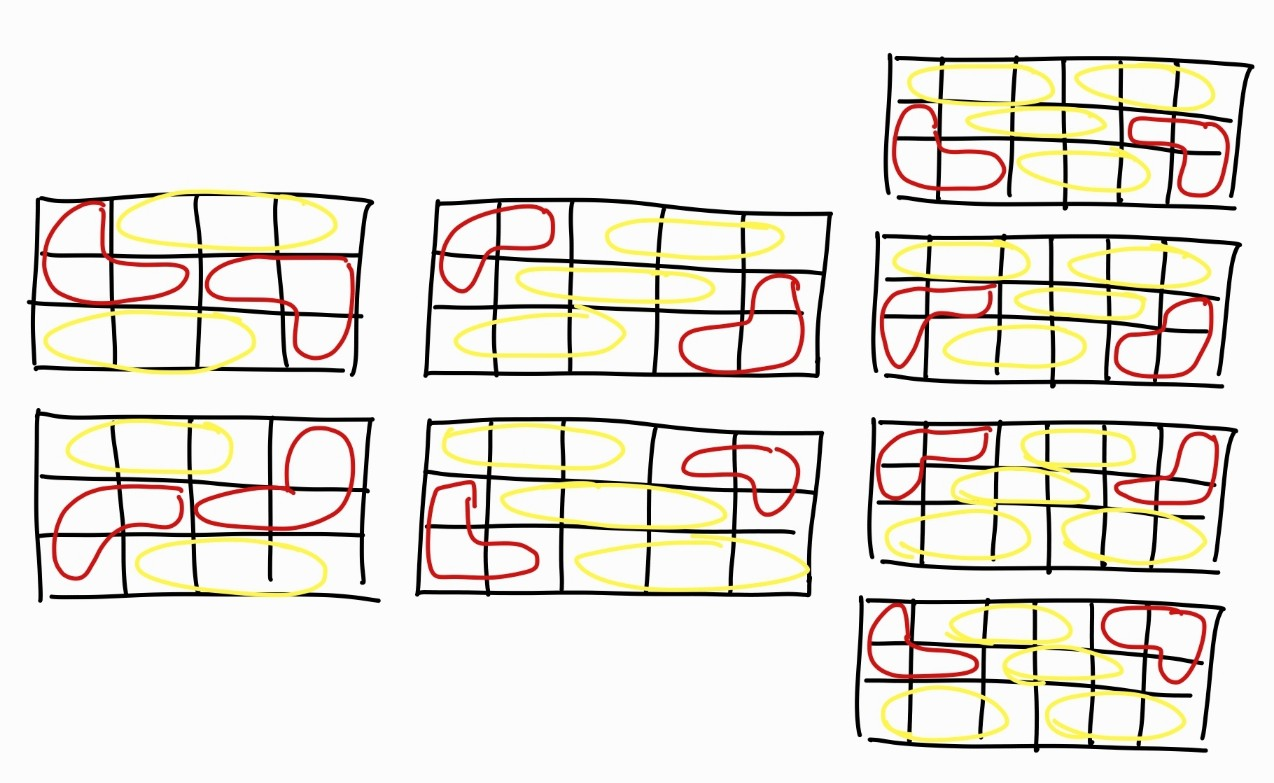
2개의 정보를 다 합하면 아래와 같은 점화식을 구할 수 있다.
$$ f(x) = f(x-1) + 2\times f(x-2) + 5 \times f(x-3) + 2 \times f(x-4) + 2 \times f(x-5) + 4 \times f(x-6) + \ldots $$
3개씩(2,2,4) 수식이 반복되기 때문에 f(x+3)을 활용하여 점화식을 정리한다.
$$ f(x+3) = f(x+2) + 2\times f(x+1) + 5 \times f(x) + 2 \times f(x-1) + 2 \times f(x-2) + 4 \times f(x-3) + \ldots $$
\( f(x) - f(x+3) \)을 해주면 아래와 같이 식을 정리할 수 있다.
$$f(x+3) = f(x+2) + 2\times f(x+1) + 6 \times f(x) + \times f(x-1) - \times f(x-3)$$
$$f(x)=f(x-1)+2\times f(x-2)+6\times f(x-3)+\times f(x-4)-\times f(x-6)$$
def solution(n):
tile = [1, 1, 3, 10, 23, 62]
if n < 6:
return tile[n]
for i in range(6, n+1):
tile.append((tile[i - 1] + 2*tile[i - 2] + 6*tile[i - 3] + tile[i - 4] - tile[i - 6]) % 1000000007)
return tile[-1]
'Coding Test > programmers' 카테고리의 다른 글
| [Python] 파이썬 프로그래머스 베스트 앨범 (0) | 2023.05.01 |
|---|---|
| [Python] 파이썬 프로그래머스 할인 행사 (0) | 2023.05.01 |
| [SQL] 프로그래머스 중복 제거하기 (0) | 2023.04.19 |
| [SQL] MySQL 프로그래머스 동물 수 구하기 (0) | 2023.04.19 |
| [SQL] MySQL 프로그래머스 최솟값 구하기 (0) | 2023.04.19 |
프로그래머스
코드 중심의 개발자 채용. 스택 기반의 포지션 매칭. 프로그래머스의 개발자 맞춤형 프로필을 등록하고, 나와 기술 궁합이 잘 맞는 기업들을 매칭 받으세요.
programmers.co.kr
나의 풀이
n별 타일 개수 구하기
2xn 타일링과 결이 비슷한 문제로 dp를 활용하여 문제를 해결했다.

nx3 (n <=3), 의 타일이 있고 그중 일부만 가져오면 아래의 모습과 같다.

1x3 타일을 1로 2x3 타일을 2로 3x3 타일을 3으로 표현하면,
3x3의 면적을 채우는 타일의 경우의 수는 아래와 같은 방식으로 구할 수 있다.
3x3
(1, 1, 1) -> 1
(1, 2), (2, 1) -> 2x2
(3) -> 5
타일의 개수 = 10

2x3 타일은 경우의 수가 2가 나오기 때문에 2를 곱해준다.

3x3타일은 경우의 수가 5개 나오기 때문에 5를 곱해준다.

규칙 찾기
위의 규칙만 따지면 \( f(x) = f(x-1) + 2\times f(x-2) + 5 \times f(x-3) \)해주면 되지만 고려해야 하는 것이 하나 더 있다.
n이 커짐에 따라 규칙이 늘어난다는 것이고 아래의 규칙을 가진다.
4x3 (4) -> 2
5x3 (5) -> 2
6x3 (6) -> 4
7x3 (7) -> 2
8x3 (8) -> 2
9x3 (9) -> 4

2개의 정보를 다 합하면 아래와 같은 점화식을 구할 수 있다.
$$ f(x) = f(x-1) + 2\times f(x-2) + 5 \times f(x-3) + 2 \times f(x-4) + 2 \times f(x-5) + 4 \times f(x-6) + \ldots $$
3개씩(2,2,4) 수식이 반복되기 때문에 f(x+3)을 활용하여 점화식을 정리한다.
$$ f(x+3) = f(x+2) + 2\times f(x+1) + 5 \times f(x) + 2 \times f(x-1) + 2 \times f(x-2) + 4 \times f(x-3) + \ldots $$
\( f(x) - f(x+3) \)을 해주면 아래와 같이 식을 정리할 수 있다.
$$f(x+3) = f(x+2) + 2\times f(x+1) + 6 \times f(x) + \times f(x-1) - \times f(x-3)$$
$$f(x)=f(x-1)+2\times f(x-2)+6\times f(x-3)+\times f(x-4)-\times f(x-6)$$
def solution(n):
tile = [1, 1, 3, 10, 23, 62]
if n < 6:
return tile[n]
for i in range(6, n+1):
tile.append((tile[i - 1] + 2*tile[i - 2] + 6*tile[i - 3] + tile[i - 4] - tile[i - 6]) % 1000000007)
return tile[-1]
'Coding Test > programmers' 카테고리의 다른 글
| [Python] 파이썬 프로그래머스 베스트 앨범 (0) | 2023.05.01 |
|---|---|
| [Python] 파이썬 프로그래머스 할인 행사 (0) | 2023.05.01 |
| [SQL] 프로그래머스 중복 제거하기 (0) | 2023.04.19 |
| [SQL] MySQL 프로그래머스 동물 수 구하기 (0) | 2023.04.19 |
| [SQL] MySQL 프로그래머스 최솟값 구하기 (0) | 2023.04.19 |
