728x90
최대공약수
GCD (Greatest Common Divisor)
두 수 이상의 공통의 약수 중 최대인 수
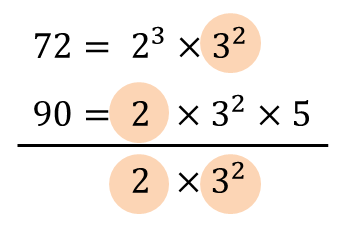
위의 경우 72와 90의 최대공약수는 18이다.
gcd = 1이라면 서로소 관계에 있다고 표현한다.
최대공배수
LCM (Least Common Multiple)
두 수 이상의 수들의 공통인 배수 중 최소인 수
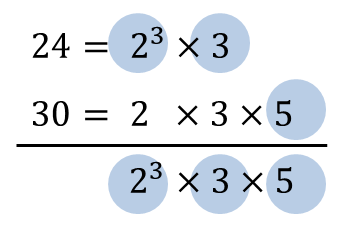
위의 경우 24, 30의 최대공배수는 120이 나온다.
구현
최소공약수
def solution(a, b):
for i in range(min(a,b),0,-1):
if a%i == 0 and b%i == 0:
return i
최대공배수
def solution(a, b):
for i in range(max(a,b),(a*b)+1):
if i%a == 0 and i%b == 0:
return i구해야하는 수가 많다면 arguments를 사용하여 list로 받아서 코드를 변경하여 사용하면 된다.
Math
math 라이브러리를 사용하여 최대 공약수 구하기
import math
#최소공약수
print(math.gcd(10,20))
print(math.gcd(15,20,30))
#최대공약수
print(math.lcm(10,20))
print(math.lcm(15,20,30))728x90
'Python > 구현' 카테고리의 다른 글
| [Python] Stack 구현하기 (0) | 2023.03.31 |
|---|---|
| NO 내장 함수 2진수 곱셈 코드 (0) | 2021.11.07 |
728x90
최대공약수
GCD (Greatest Common Divisor)
두 수 이상의 공통의 약수 중 최대인 수
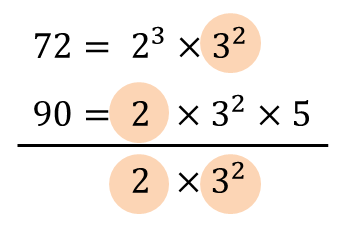
위의 경우 72와 90의 최대공약수는 18이다.
gcd = 1이라면 서로소 관계에 있다고 표현한다.
최대공배수
LCM (Least Common Multiple)
두 수 이상의 수들의 공통인 배수 중 최소인 수
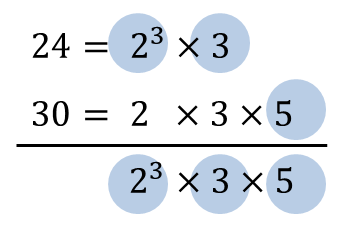
위의 경우 24, 30의 최대공배수는 120이 나온다.
구현
최소공약수
def solution(a, b):
for i in range(min(a,b),0,-1):
if a%i == 0 and b%i == 0:
return i
최대공배수
def solution(a, b):
for i in range(max(a,b),(a*b)+1):
if i%a == 0 and i%b == 0:
return i구해야하는 수가 많다면 arguments를 사용하여 list로 받아서 코드를 변경하여 사용하면 된다.
Math
math 라이브러리를 사용하여 최대 공약수 구하기
import math
#최소공약수
print(math.gcd(10,20))
print(math.gcd(15,20,30))
#최대공약수
print(math.lcm(10,20))
print(math.lcm(15,20,30))728x90
'Python > 구현' 카테고리의 다른 글
| [Python] Stack 구현하기 (0) | 2023.03.31 |
|---|---|
| NO 내장 함수 2진수 곱셈 코드 (0) | 2021.11.07 |
