신장 트리(Spanning Tree)
신장 트리란 아래의 조건을 만족하면서 모든 노드가 연결되어 있는 Tree 구조를 말함
- 모든 노트가 서로 연결되어 있어야 한다.
- 사이클이 존재하지 않아야 한다.(Tree의 속성)

왼쪽이 Original graph이고 오른쪽이 Original graph에서 나올 수 있는 신장 트리이다.
최소 신장 트리(MST)
Minimum Spanning Tree(MST)라고도 불리며 Spanning Tree의 간선 가중치 값이 최소인 Tree를 말함

최소 신장 트리 알고리즘
- 그래프에서 최소 신장 트리를 찾을 수 있는 알고리즘이 존재함
- 대표적인 최소 신장 트리 알고리즘
- Kruskal's algorithm (크루스칼 알고리즘), Prim's algorithm(프림 알고리즘)
크루스칼 알고리즘
탐욕법을 기초로 최소의 비용을 선택해서 최적의 솔루션을 찾음
1. 모든 정점을 독립적인 집합으로 만든다.
2. 모든 간선을 비용으로 기준으로 정렬하고 비용이 작은 간선부터 양 끝의 두 정점을 비교한다
3. 두 정점의 최상위 정점을 확인하고, 서로 다를 경우 두 정점을 연결한다.( 최소 신장 트리는 사이클이 없으므로, 사이클이 생기지 않도록 하는 작업)


Union-Find 알고리즘
최적의 간선을 선택할 때 사이클의 유무를 판단하는 알고리즘으로 Disjoint를 표현할 때 사용한다.
Disjoint
- 서로 중복되지 않는 부분 집합들로 나눠진 원소들에 대한 정보를 저장하고 조작하는 자료구조
- 공통 원소가 없는 상호 배타적인 부분 집합(서로소)들로 나눠진 원소들에 대한 자료구조를 의미함
1. 초기화 - n개의 원소가 개별 집합으로 이뤄지도록 초기화한다.

2. Union - 두 개별 집합을 하나의 집합으로 합쳐 두 개의 트리를 하나의 트리로 만든다.

3. Find 여러 노드가 존재할 때, 두 개의 노드를 선택해서, 두 노드가 서로 같은 그래프에 속하는지 루트 노트를 확인하여 판별한다.

Union-Find는 한 가지 문제가 존재하는데 그것은 최악의 경우 tree가 깊어져 find 과정에서 \( O(n) \)의 시간복잡도를 가질 수 있다는 것이다. 이를 해결하기 위해, Union-by-rank, path compression 기법을 사용한다.
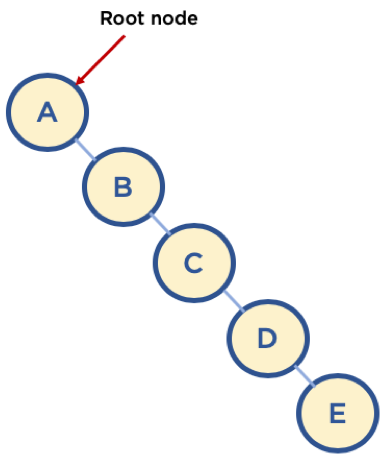
Union-by-rank 기법
각 트리의 rank를 기억하고 Union시 트리의 높이가 다르면 높이가 작은 트리를 높이가 큰 트리에 붙이는 기법으로 tree가 깊어지는 것을 방지할 수 있고 높이가 같은 2개의 트리를 합칠 때, 한쪽의 트리의 높이를 1 증가시키고 다른 쪽의 트리를 높이 트리에 붙여준다.



- 초기화 시, 모든 rank가 0인 개별 집합 상태에서, 하나씩 원소를 합친다고 할 때
- 높이가 h인 트리를 만들기 위해서는 높이가 h-1인 트리를 합쳐야 한다.
- 높이가 h-1인 트리를 만들기 위해 최소 n 개의 원소가 필요하다면, 높이가 h인 트리를 만들기 위해서는 최소 2n개의 원소가 필요하고 따라서 union-by-rank를 사용하면 union, find 과정의 시간복잡도를 \( O(logN) \)으로 낮출 수 있다.
Path compression기법
find를 실행한 노드에서 거쳐간 노드를 루트에 다이렉트로 연결하는 기법으로 find 실행 이후 루트 노드를 한 번에 할 수 있다.

시간 복잡도
Union-by-rank와 path compression을 이용하여 시간 복잡도는 다음과 같은 계산식이 나옴
$$ O(MlogN) $$
N이 아무리 큰 수가 나오더라도 \( logN \)의 시간복잡도를 가지기 때문에 거의 상수에 가까운 \( O(1) \) 시간 복잡도를 가짐
크루스칼을 초기화, 정렬, 간선 선택 3가지 함수가 존재한다.
초기화
- node의 갯수 만큼 반복문이 돌아간다
- \(O(V) \) V는node의 개수
정렬
- 간선의 Weight를 기준으로 간선을 정렬하고 고급 정렬(\( O(n logn) \))을 사용함
- \( O(ElogE) \)
간선 선택
- 간선의 개수 만큼 반복문이 돌아감
- \( O(E) \)
- 노드를 체크하여 사이클이 생기지 않도록 하는데 path compression 등 최적화 기법을 사용함
- \( O(1) \)
-> 크루스칼은 결국 정렬 알고리즘인 \( O(ElogE) \) 의 시간 복잡도를 따른다.
실습

위의 graph에서 최소 신장 트리를 크루스칼을 이용하여 구하고 그 내용을 구현함
mygraph = {
'vertices': ['A', 'B', 'C', 'D', 'E', 'F', 'G'],
'edges': [
(7, 'A', 'B'),
(5, 'A', 'D'),
(7, 'B', 'A'),
(8, 'B', 'C'),
(9, 'B', 'D'),
(7, 'B', 'E'),
(8, 'C', 'B'),
(5, 'C', 'E'),
(5, 'D', 'A'),
(9, 'D', 'B'),
(7, 'D', 'E'),
(6, 'D', 'F'),
(7, 'E', 'B'),
(5, 'E', 'C'),
(7, 'E', 'D'),
(8, 'E', 'F'),
(9, 'E', 'G'),
(6, 'F', 'D'),
(8, 'F', 'E'),
(11, 'F', 'G'),
(9, 'G', 'E'),
(11, 'G', 'F')
]
}parent = dict()
rank = dict()
def find(node):
#path compression
if parent[node] != node:
parent[node]=find(parent[node])
return parent[node]
def union(node_v, node_u):
root1 = find(node_v)
root2 = find(node_u)
if rank[root1]>rank[root2]:
parent[root2] = root1
else:
parent[root1] = root2
if rank[root1] == rank[root2]:
rank[root2]+=1
def make_set(node): # 모든 node를 root node로 만듦
parent[node] = node
rank[node] = 0
def kruskal(graph):
# 선택된 간선만 넣음
mst = list()
# 1. 초기화
for node in graph['vertices']:
make_set(node) # 독립적인 집합으로 만듦
# 2. 간선 weight 기반 Sorting
edges = graph['edges'] #간선의 weight와 간선 정보를 가지고 있음
edges.sort()
# 3. 사이클 없는 간선
for edge in edges: #탐욕법 가장 작은 weight 부터
weight, node_v, node_u = edge
if find(node_v) != find(node_u): #사이클을 탐색함, 둘의 root node가 같다면 사이클이 생기는 것
union(node_v, node_u)
mst.append(edge)
return mst
'자료구조&알고리즘' 카테고리의 다른 글
| [알고리즘] 백트래킹(Backtracking) (0) | 2023.04.10 |
|---|---|
| [알고리즘] 최단 경로 - 다익스트라 (0) | 2022.11.21 |
| [알고리즘] 탐욕 알고리즘 Greedy (0) | 2022.11.12 |
| [알고리즘] 깊이 우선 탐색 DFS Depth First Search (0) | 2022.11.07 |
| [알고리즘] 너비 우선 탐색 BFS Breadth First Search (0) | 2022.11.05 |
