728x90
Generation model의 학습방법을 이해하기 위해서 알고 가야함
생성 모델의 개념
- 확률 변수 (Random variable): 시행의 결과에 따라 값이 결정되는 변수
- 확률 질량 함수 (Probability mass function): 이산 확률 변수 x의 분포를 나타내는 함수로, 함수 값이 곧 확률임
- 확률 밀도 함수 (Probability density function) : 연속 확률 변수 x의 분포를 나타내는 함수로, 밀도의 넓이가 곧 확률임
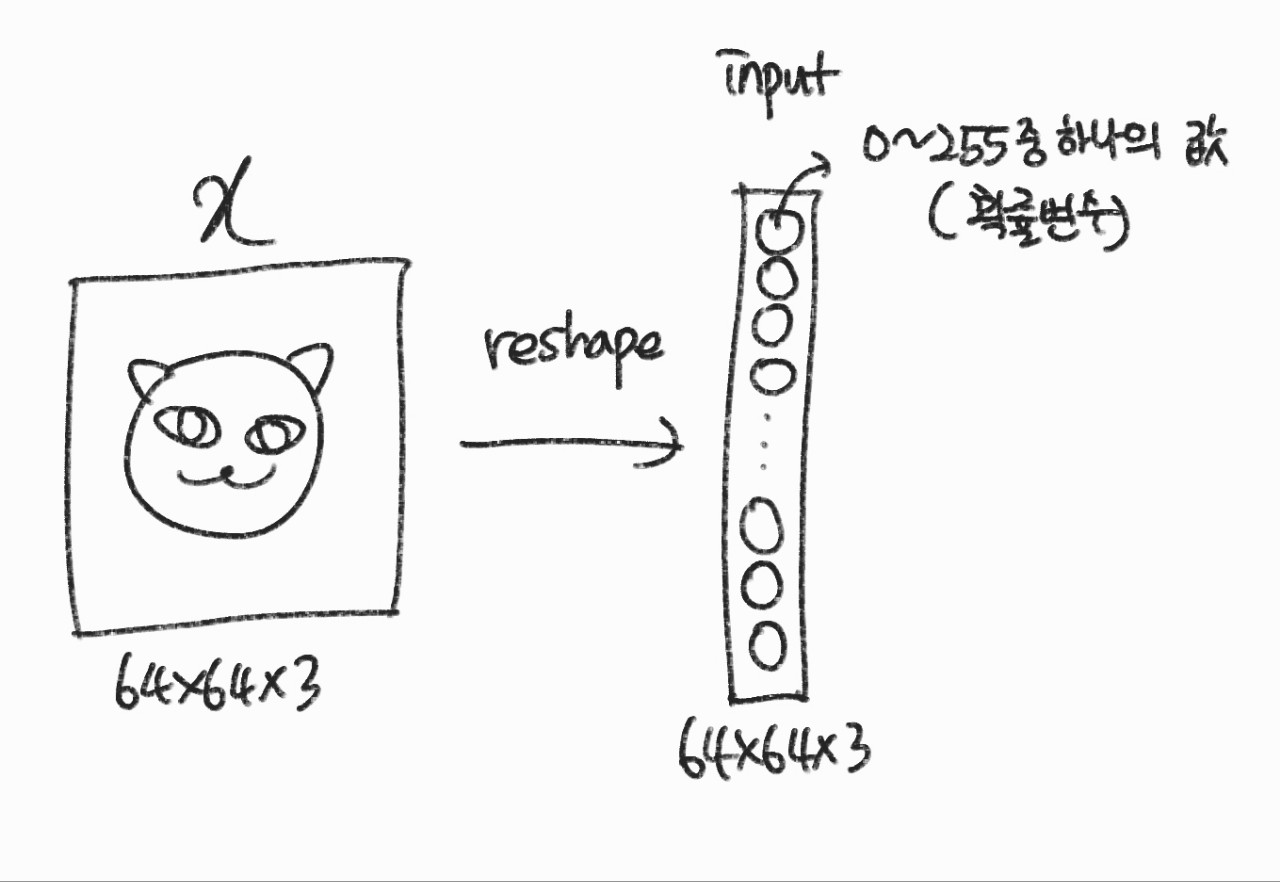
- input data를 확률 변수로 본다면 64 x 64 x 3의 차원을 가지는 벡터로 표현될 수 있음
- 각각 64 x 74 x 3 벡터의 확률값을 추정해볼 수 있음
- Pdata(x)는 확률 밀도 함수로 실제 이미지들의 정확한 분포를 나타내고 우리는 이와 비슷한 분포를 가지는 생성 모델을 만들어야함
- 아래는 추정 벡터가 1 Dimension일 경우

- \( x_{1} \) : 3색을 가지고 있는 고양이가 포함되어 있을 수 있음, (\(x_{1}\)은 3색 고양이를 나타내는 고차원 벡터(64 x 64 x 3 ))
- \( x_{2} \) : 검은색을 가지고 있는 고양이가 포함되어 있을 수 있음, (\(x_{2}\)은 검은색 고양이를 나타내는 고차원 벡터(64 x 64 x 3 ))
- \( x_{3} \) : 흰색을 가지고 있는 고양이가 포함되어 있을 수 있음, (\(x_{3}\)은 흰색 고양이를 나타내는 고차원 벡터(64 x 64 x 3 ))
생성모델은 Pdata(x)를 잘 근사하는 Pmodel(x)을 찾는 것이 목표이다.
728x90
'Generative model' 카테고리의 다른 글
| [GAN] GAN 학습 (1) | 2022.12.29 |
|---|---|
| [GAN] 생성 모델 GAN의 이해 (0) | 2022.12.29 |
| [GAN] GANs Generative Adversarial Networks (0) | 2022.12.26 |
| [VAE] Variational AutoEncoder (0) | 2022.10.14 |
| [GAN] Computer vision (0) | 2022.10.14 |
