728x90
계산 복잡도
- 시간 복잡도 Time Complexity: 얼마나 빠른지 (속도), 알고리즘에 사용되는 연산 횟수의 총량
- 공간 복잡도 Space Complexity : 얼마나 많은 저장공간이 필요한지(메모리), 알고리즘에 사용되는 메모리 공간의 총량
- 시간 복잡도와 공간 복잡도는 반비례적인 성향을 띄고 있음
- 최근 대용량 시스템이 보편화 되면서 시간 복잡도를 우선시 함 (빅 데이터를 다룰때 공간 복잡도 또한 신경씀)
필요한 이유
- 하나의 문제를 푸는 알고리즘은 다양할 수 있는데 어느 알고리즘이 더 좋은지 분석해봐야함
- 이 때 사용하는 것이 계산 복잡도임
예시) 절대값 구하기
- 정수값 제곱 후 루트
- 음수일 때, -1 곱하기
등 다양한 풀이법이 나옴 간단한 문제라 복잡도에 차이가 없음
알고리즘 성능 표기법
Big O (빅 오) 표기법: \( O(n) \)
- 알고리즘 가장 최악을 실행 시간을 표기함 -> 최악을 상황일 때, 최대의 성능을 보여줌
- 일반적으로 가장 많이 사용함
\( \Omega \) 표기법: \( \Omega(n) \)
- 알고리즘 최상의 실행 시간을 표기함
\( \Theta \) 표기법: \( \Theta(n) \)
- 알고리즘의 평균 실행 시간을 표기함
빅 오 표기법
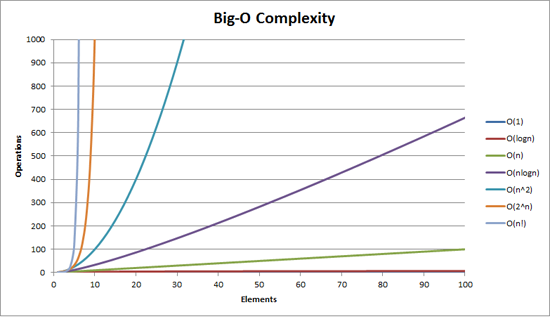
- O(입력)
- O(1), O(\( logn \)), O(n), O(n\( logn \)), O(\( n^{2} \)), O(\( 2^{n} \)), O(n!)
- O(1) < O(\( logn \)) < O(n) < O(n\( logn \)) < O(\( n^{2} \)) < O(\( 2^{n} \)) < O(n!)
- \( logn \) -> \( log_{2}n \)
시간 복잡도
- 알고리즘의 실행 속도
- 반복문을 가지고 시간 복잡도를 계산함
- 프로그램 실행 중 반복문이 수행 시간에 영향을 가장 많이 미치기 때문
- 표현식에 가장 큰 영향을 미치는 n의 단위를 표기함
- n이 1, 100, 1000, 10000이든 이 경우에는 상수가 들어가기 때문에 O(1)이다.
- n이 n, n + 10, 3n + 1000이든 이 경우에는 O(n)이다.
예제: 1부터 n까지 합 구하기
#1
- 1부터 n까지 반복문을 만들어 더하기
def sum_num(n):
sum_total = 0
for i in range(1, n+1):
sum_total += i
return sum_totalO(n)
#2
- \( \frac{n(n+1)}{2} \)
def sum_num(n):
return n*n(n+1)/2O(1)
공간 복잡도
- 옛날에는 공간 복잡도도 고려해야했기 때문에 알고리즘 문제에서 고려해야할 경우가 있음
- 기존 알고리즘 문제가 공간 복잡도에 영향을 받아서 면접시 중요하게 생각하는 부분도 있음
- 프로그램을 실행 및 완료하는데 필요한 저장 공간의 양
- 총 필요 저장 공간
- 고정 공간: 코드 저장, 단순 변수 및 상수 저장 (알고리즘 실행과는 무관)
- 가변 공간: 실행 중 동적으로 필요한 공간 (알고리즘 실행과 관련있음)
- \( S(P) = c+S_{p}(n) \)
- \( c \): 고정 공간
- \( S_{p}(n) \): 가변 공간
- 빅 오 표기법에서, 고정 공간은 상수이기 때문에 해당이 안됨
예제 : n! 팩토리얼 구하기
- n! = 1 x 2 x ... x n
#1
- n의 값에 상관없이 변수 n, 변수 fac, 변수 index만 필요 -> 공간 복잡도: \( O(1) \)
def facto(n):
fac = 1
for index in range(2, n+1):
fac = fac * index
return fac
#2
- 재귀함수 사용 -> n에 따라 변수 n이 n개 만들어짐 -> 공간 복잡도: \( O(n) \)
def facto(n):
if n>1:
return n*facro(n-1)
else:
return 1728x90
'자료구조&알고리즘' 카테고리의 다른 글
| [알고리즘] 병합 정렬 merge sort (0) | 2022.10.28 |
|---|---|
| [알고리즘] 퀵 정렬 Quick sort (0) | 2022.10.14 |
| [알고리즘] 기본 정렬 ( 버블 정렬, 삽입 정렬, 선택 정렬) (0) | 2022.10.12 |
| [알고리즘] 순차 탐색 Sequential Search (0) | 2022.10.10 |
| [알고리즘] 이진 탐색 Binary Search (0) | 2022.10.10 |
